Развернуть задание
Дан куб ABCDA1B1C1D1. Найдите следующие двугранные углы:
а) ABB1C
б) ADD1B
в) A1BB1K, где K – середина ребра A1D1
а) ABB1C
б) ADD1B
в) A1BB1K, где K – середина ребра A1D1
Развернуть задание
Новое решение
Решение
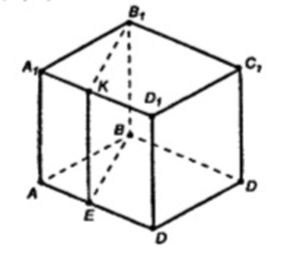
а) ∠A1B1C1 – линейный угол двугранного угла ABB1C, ∠A1B1C1 = 90˚, т.к. данная фигура - куб.
б) Необходимо найти угол между плоскостями AA1D1D и BDD1B.
∠ADB – линейный угол двугранного угла ADD1B, ∠ADB = 45˚.
в) Проведем B1K; Проведем KE || AA1; Проведем диагональ квадрата BE.
Найдем линейную меру двугранного угла между плоскостями AA1B1B и KB1BE. A1B1 ⊥ BB1.
б) Необходимо найти угол между плоскостями AA1D1D и BDD1B.
∠ADB – линейный угол двугранного угла ADD1B, ∠ADB = 45˚.
в) Проведем B1K; Проведем KE || AA1; Проведем диагональ квадрата BE.
Найдем линейную меру двугранного угла между плоскостями AA1B1B и KB1BE. A1B1 ⊥ BB1.
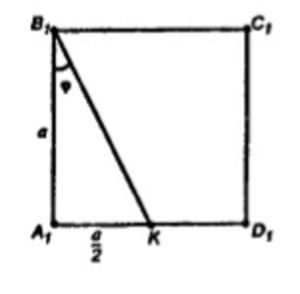
Таким образом ∠A1B1K – линейный угол двугранного угла ABB1K.
Пусть ребро куба равно a, тогда tg φ = 1/2 => φ = arctg 1/2
Ответ: а) 90˚, б) 45˚, в) arctg 1/2
Пусть ребро куба равно a, тогда tg φ = 1/2 => φ = arctg 1/2
Ответ: а) 90˚, б) 45˚, в) arctg 1/2

а) ∠A1B1C1 – линейный угол двугранного угла ABB1C, ∠A1B1C1 = 90˚, т.к. данная фигура - куб.
б) Необходимо найти угол между плоскостями AA1D1D и BDD1B.
∠ADB – линейный угол двугранного угла ADD1B, ∠ADB = 45˚.
в) Проведем B1K; Проведем KE || AA1; Проведем диагональ квадрата BE.
Найдем линейную меру двугранного угла между плоскостями AA1B1B и KB1BE. A1B1 ⊥ BB1.
б) Необходимо найти угол между плоскостями AA1D1D и BDD1B.
∠ADB – линейный угол двугранного угла ADD1B, ∠ADB = 45˚.
в) Проведем B1K; Проведем KE || AA1; Проведем диагональ квадрата BE.
Найдем линейную меру двугранного угла между плоскостями AA1B1B и KB1BE. A1B1 ⊥ BB1.

Таким образом ∠A1B1K – линейный угол двугранного угла ABB1K.
Пусть ребро куба равно a, тогда tg φ = 1/2 => φ = arctg 1/2
Ответ: а) 90˚, б) 45˚, в) arctg 1/2
Пусть ребро куба равно a, тогда tg φ = 1/2 => φ = arctg 1/2
Ответ: а) 90˚, б) 45˚, в) arctg 1/2