Задание
Развернуть задание
Точка C лежит на отрезке AB. Через точку A проведена плоскость, а через точки B и C – параллельные прямые, пересекающие эту плоскость соответственно в точках B1 и C1. Найдите длину отрезка CC1, если точка C – середина отрезка AB и BB1 = 7 см.
Развернуть задание
Новое решение
Решение
- Предыдущее
- Следующее
Мы вправе рассматривать ∆CAC1 и ∆BAB1, так как они лежат в одной плоскости (из параллельности BB1 и CC1 следует, что эти отрезки лежат в одной плоскости β. Тогда C ∈ β и B ∈ β => BC лежит на β. Значит, прямые BB1, CC1 и AB лежат на β)
∆CAC1 ~ ∆BAB1 (по двум углам) (углы B1BA, С1СА соответственно равны, а угол САС1 – общий)
Из подобия имеем:
CC1/BB1 = AC/AB;
Так как С – середина отрезка АВ, то AC/AB = ½, и получим:
CC1/7 = 1/2
Откуда CC1 = 3.5
Ответ: 3.5
∆CAC1 ~ ∆BAB1 (по двум углам) (углы B1BA, С1СА соответственно равны, а угол САС1 – общий)
Из подобия имеем:
CC1/BB1 = AC/AB;
Так как С – середина отрезка АВ, то AC/AB = ½, и получим:
CC1/7 = 1/2
Откуда CC1 = 3.5
Ответ: 3.5
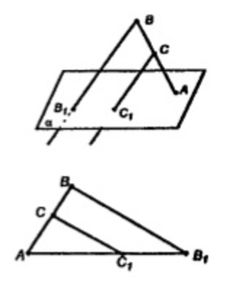
Мы вправе рассматривать ∆CAC1 и ∆BAB1, так как они лежат в одной плоскости (из параллельности BB1 и CC1 следует, что эти отрезки лежат в одной плоскости β. Тогда C ∈ β и B ∈ β => BC лежит на β. Значит, прямые BB1, CC1 и AB лежат на β)
∆CAC1 ~ ∆BAB1 (по двум углам) (углы B1BA, С1СА соответственно равны, а угол САС1 – общий)
Из подобия имеем:
CC1/BB1 = AC/AB;
Так как С – середина отрезка АВ, то AC/AB = ½, и получим:
CC1/7 = 1/2
Откуда CC1 = 3.5
Ответ: 3.5
∆CAC1 ~ ∆BAB1 (по двум углам) (углы B1BA, С1СА соответственно равны, а угол САС1 – общий)
Из подобия имеем:
CC1/BB1 = AC/AB;
Так как С – середина отрезка АВ, то AC/AB = ½, и получим:
CC1/7 = 1/2
Откуда CC1 = 3.5
Ответ: 3.5
