Задание
Развернуть задание
Точки A и B лежат в плоскости α, а точка C не лежит в этой плоскости. Докажите, что прямая, проходящая через середины отрезков AC и BC, параллельны плоскости α.
Развернуть задание
Новое решение
Решение
- Предыдущее
- Следующее
Рассмотрим ∆ABC. В нём, по условию, MN – прямая, проходящая через середины сторон AC и CB. В ∆ABC MN будет средней линией, а по свойству средней линии (средняя линия параллельна основанию), получим, что MN || AB. По теореме о параллельности прямой и плоскости (если прямая, не лежащая в данной плоскости, параллельна прямой, лежащей в этой плоскости, то она параллельна данной плоскости), получим, что MN || α
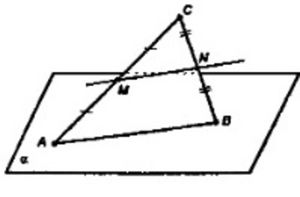
Рассмотрим ∆ABC. В нём, по условию, MN – прямая, проходящая через середины сторон AC и CB. В ∆ABC MN будет средней линией, а по свойству средней линии (средняя линия параллельна основанию), получим, что MN || AB. По теореме о параллельности прямой и плоскости (если прямая, не лежащая в данной плоскости, параллельна прямой, лежащей в этой плоскости, то она параллельна данной плоскости), получим, что MN || α
