Задание
Развернуть задание
Докажите, что если данная прямая параллельна прямой, по которой пересекаются две плоскости, и не лежит в этих плоскостях, то она параллельна этим плоскостям.
Развернуть задание
Новое решение
Решение
Рассмотрим прямую MN, по которой пересекаются плоскости α и β. Как видно, прямая MN принадлежит как одной плоскости, так и другой.
Рассмотрим MN, как прямую, принадлежащую плоскости α. По условию, l || MN, а так как MN лежит в плоскости α, значит по теореме о параллельности прямой и плоскости (если прямая, не лежащая в данной плоскости, параллельна прямой, лежащей в этой плоскости, то она параллельна данной плоскости), получим, что l || α.
Рассмотрим MN, как прямую, принадлежащую плоскости β. По условию, l || MN, а так как MN лежит в плоскости β, значит по теореме о параллельности прямой и плоскости (если прямая, не лежащая в данной плоскости, параллельна прямой, лежащей в этой плоскости, то она параллельна данной плоскости), получим, что l || β.
Рассмотрим MN, как прямую, принадлежащую плоскости α. По условию, l || MN, а так как MN лежит в плоскости α, значит по теореме о параллельности прямой и плоскости (если прямая, не лежащая в данной плоскости, параллельна прямой, лежащей в этой плоскости, то она параллельна данной плоскости), получим, что l || α.
Рассмотрим MN, как прямую, принадлежащую плоскости β. По условию, l || MN, а так как MN лежит в плоскости β, значит по теореме о параллельности прямой и плоскости (если прямая, не лежащая в данной плоскости, параллельна прямой, лежащей в этой плоскости, то она параллельна данной плоскости), получим, что l || β.
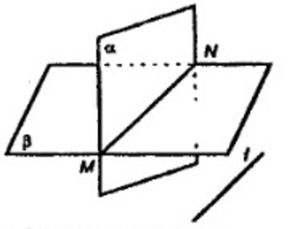
Рассмотрим прямую MN, по которой пересекаются плоскости α и β. Как видно, прямая MN принадлежит как одной плоскости, так и другой.
Рассмотрим MN, как прямую, принадлежащую плоскости α. По условию, l || MN, а так как MN лежит в плоскости α, значит по теореме о параллельности прямой и плоскости (если прямая, не лежащая в данной плоскости, параллельна прямой, лежащей в этой плоскости, то она параллельна данной плоскости), получим, что l || α.
Рассмотрим MN, как прямую, принадлежащую плоскости β. По условию, l || MN, а так как MN лежит в плоскости β, значит по теореме о параллельности прямой и плоскости (если прямая, не лежащая в данной плоскости, параллельна прямой, лежащей в этой плоскости, то она параллельна данной плоскости), получим, что l || β.
Рассмотрим MN, как прямую, принадлежащую плоскости α. По условию, l || MN, а так как MN лежит в плоскости α, значит по теореме о параллельности прямой и плоскости (если прямая, не лежащая в данной плоскости, параллельна прямой, лежащей в этой плоскости, то она параллельна данной плоскости), получим, что l || α.
Рассмотрим MN, как прямую, принадлежащую плоскости β. По условию, l || MN, а так как MN лежит в плоскости β, значит по теореме о параллельности прямой и плоскости (если прямая, не лежащая в данной плоскости, параллельна прямой, лежащей в этой плоскости, то она параллельна данной плоскости), получим, что l || β.
