Задание
Развернуть задание
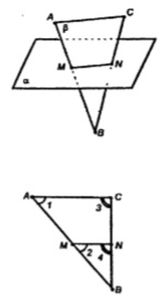
Сторона AC треугольника ABC параллельна плоскости α, а стороны AB и BC пересекаются с этой плоскостью в точках M и N. Докажите, что треугольники ABC и MBN подобны.
Развернуть задание
Новое решение
Решение
AC лежит в плоскости ABC (AC || α), и ABC пересекает α, линия пересечения MN параллельна прямой AC. Значит MN || AC
∠1 = ∠2, как соответственные углы, ∠ABC – общий =>
∆ABC ~ ∆MBN (по двум равным углам)
∠1 = ∠2, как соответственные углы, ∠ABC – общий =>
∆ABC ~ ∆MBN (по двум равным углам)
