Задание
Развернуть задание
Точка C лежит на отрезке AB, причем, AB : BC = 4 : 3. Отрезок CD = 12 см, параллелен плоскости α, проходящей через точку B. Докажите, что прямая AD пересекает плоскость α в некоторой точке E, и найдите отрезок BE.
Развернуть задание
Новое решение
Решение
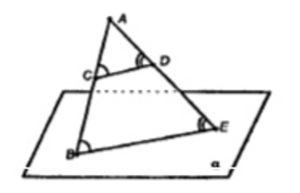
AB/BC = 4/3, CD || α, CD = 12.
Так как B – общая точка, то плоскости ABE и α пересекаются. Из теоремы 2 CD || BE.
Так как B – общая точка, то плоскости ABE и α пересекаются. Из теоремы 2 CD || BE.
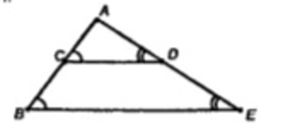
∠1 = ∠2, ∠3 = ∠4, как соответственные => ∆ABE ~ ∆ACD по двум углам. Из подобия имеем:
AB/AC = BE/CD
(AB – BC)/AB = 12/BE
1 – 3/4 = 12/BE
BE = 48
AB/AC = BE/CD
(AB – BC)/AB = 12/BE
1 – 3/4 = 12/BE
BE = 48

AB/BC = 4/3, CD || α, CD = 12.
Так как B – общая точка, то плоскости ABE и α пересекаются. Из теоремы 2 CD || BE.
Так как B – общая точка, то плоскости ABE и α пересекаются. Из теоремы 2 CD || BE.

∠1 = ∠2, ∠3 = ∠4, как соответственные => ∆ABE ~ ∆ACD по двум углам. Из подобия имеем:
AB/AC = BE/CD
(AB – BC)/AB = 12/BE
1 – 3/4 = 12/BE
BE = 48
AB/AC = BE/CD
(AB – BC)/AB = 12/BE
1 – 3/4 = 12/BE
BE = 48