Задание
Развернуть задание
На сторонах AB и AC треугольника ABC взяты соответственно точки D и E так, что длина отрезка DE равна 5 см и BD/DA = 2/3. Плоскость α проходит через точки B и С и параллельна отрезку DE. Найдите длину отрезка BC.
Развернуть задание
Новое решение
Решение
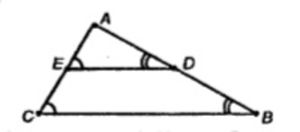
DE = 5, BD/DA = 2/3
DE || α, DE лежит в плоскости ABC
∆BAC ~ ∆DAE (по двум углам). Из подобия имеем:
BC/DE = AB/AD = 1 + DB/AD
BC/5 = 1 + 2/3 = 5/3
BC = 8 1/3
DE || α, DE лежит в плоскости ABC
∆BAC ~ ∆DAE (по двум углам). Из подобия имеем:
BC/DE = AB/AD = 1 + DB/AD
BC/5 = 1 + 2/3 = 5/3
BC = 8 1/3
