Решения
Алиса


30-11-2016 20:21

0
Задания
Задание

Дмитрий
30-11-2016
16:48
Школа

Геометрия

10 класс


10
1
0
0

Параллельность прямой и плоскости, признаки и свойства

Доказать, что плоскость пересекает отрезок в точке, и найти расстояние от этой точки до точки на плоскости.

Развернуть задание
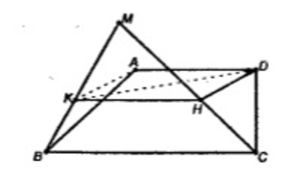
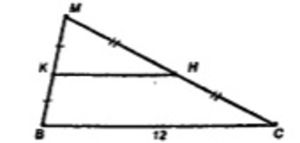
В трапеции ABCD основание BC равно 12 см. Точка M не лежит в плоскости трапеции, а точка K – середина отрезка BM. Докажите, что плоскость ADK пересекает отрезок MC в некоторой точке H, и найдите отрезок KH.
Сергей Геннадиевич
Новый коммент
24-07-2017 17:41:17
Алиса
Судя по таблице удельной теплоёмкости, это может быть цинк.
22-11-2016 12:57:23
Анастасия
Дмитрий Да, перевод обязателен.
21-11-2016 19:00:39
Дмитрий
1) –Обязательно ли переводить массу мяча в СИ?
21-11-2016 18:51:12
Рогова Дарья
Условие смущает. Ладно, пусть время будет отрицательным, наблюдать можно с любого момента, но не ясно, каким моментам времени соответствуют моменты изменения скорости. Можно предположить, что первый пик где-то в районе -1,5 с, но так ли это?.. Третий пик вообще без координатной сетки не определишь. И еще: график чего именно надо построить? МОДУЛЯ скорости или ПРОЕКЦИИ скорости?
3-11-2016 00:11:19
Андрей Анатольевич
Почему картика в блоке так размыта? А при просмотре в правой части (крупно) все выглядит гораздо лучше. Как то плохо пережимается картинка.
2-11-2016 15:29:02
Андрей Анатольевич
t = 20ºC или 200 С ?
31-10-2016 20:21:46
Эдуард Блохин
Интересное задание. Пригодится.
27-10-2016 14:34:02
Развернуть задание
Новое решение
Сложность
4 3 2 1
Решение
Алиса
30-11-2016 20:21:30
0
По теореме 1 AD || BMC.
Рассмотрим плоскость BMC:
H – середина MC (по т. о пропорциональных отрезках)
KH – средняя линия ∆BMC;
KH = BC/2 = 6
Олег
ValeryL -В решении просто опущено приведение к одному знаменателю. Мы вносим множитель 5 в числитель и знаменатель первой дроби, а в числитель и знаменатель второй дроби множитель 3. Получаем «5/15 + 3/15» и объединяем в одну дробь «(5 + 3) / 15».
24-11-2016 00:08:45
Алина
Лолита Лучше начать с горелки. Так ответ будет более полным.
23-11-2016 22:52:10
Лолита
Нужно описывать превращения энергии начиная с горелки или с пробирки?
23-11-2016 22:50:55
Елизавета
Екатерина По идее – да. Но, возможно, его будет не так явно видно.
23-11-2016 22:45:04
Екатерина
Этот опыт применим для любой жидкости?
23-11-2016 22:43:50
Ира
Ольга Универсальная газовая постоянная. R ≈ 8,314 Дж/(моль * К)
23-11-2016 22:31:43
Ольга
Что такое R в формуле?
23-11-2016 22:30:53
Елизавета
почему мы ищем число отрезков по 0,5 см?
23-11-2016 22:08:54
Елизавета
почему , чем ближе к Земле, тем больше скорость?
23-11-2016 22:05:53
Елизавета
почему путь, проеденный стрелкой, равняется 31,4?
23-11-2016 22:04:13
Елизавета
почему перемещение равно длине гипотенузы данного треугольника?
23-11-2016 22:02:09
Елизавета
почему у векторов s1,s2,s6 нулевые проекции?
23-11-2016 22:00:19
Елизавета
каким образом фиксируются точки начала и конца движения?
23-11-2016 21:58:13
Елизавета
почему самолёты неподвижны относительно друг друга?
23-11-2016 21:53:52
Елизавета
почему относительно друг друга скорость равна нулю?
23-11-2016 21:51:46
Елизавета
почему траектория движения окружность?
23-11-2016 21:49:52
Елизавета
почему именно прямая линия?
23-11-2016 21:48:17
ValeryL
Странно, что в условии не указана продолжительность урока.
23-11-2016 21:37:42
ValeryL
Почему мы не отделяем скобками выражения «154 * 25» и «76 * 30»?
23-11-2016 21:35:44
Анастасия
Диана Да, все должно измеряться в одинаковых величинах для корректного решения
23-11-2016 20:58:46
Алиса
30-11-2016 20:21:30
0
По теореме 1 AD || BMC.
Рассмотрим плоскость BMC:
H – середина MC (по т. о пропорциональных отрезках)
KH – средняя линия ∆BMC;
KH = BC/2 = 6
Новость часа

Форма обратной связи