Задание
Развернуть задание
Докажите, что если три плоскости, не проходящие через одну прямую, попарно пересекаются, то прямые, по которым они пересекаются, либо параллельны, либо имеют общую точку.
Развернуть задание
Новое решение
Решение
Пусть a не параллельна b, тогда a пересекается с b в некоторой точке K.
K ∈ γ, K ∈ α.
Тогда плоскость γ пересекается с плоскостью α не только по прямой c, но еще по второй прямой, проходящей через K.
То есть точка K ∈ c. Получили, что, либо плоскости имеют общую точку K, либо наше допущение неверно, то есть a || b. Если a || b, то a || α => a не пересекается с c, но лежит с ней в одной плоскости γ. Тогда по определению a || c || b.
В случае, когда плоскости имеют общую точку, они попарно пересекаются, образуя фигуру, называемую трехгранным углом
K ∈ γ, K ∈ α.
Тогда плоскость γ пересекается с плоскостью α не только по прямой c, но еще по второй прямой, проходящей через K.
То есть точка K ∈ c. Получили, что, либо плоскости имеют общую точку K, либо наше допущение неверно, то есть a || b. Если a || b, то a || α => a не пересекается с c, но лежит с ней в одной плоскости γ. Тогда по определению a || c || b.
В случае, когда плоскости имеют общую точку, они попарно пересекаются, образуя фигуру, называемую трехгранным углом
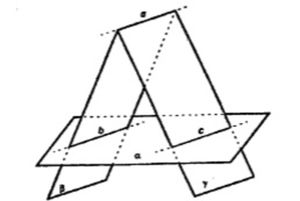
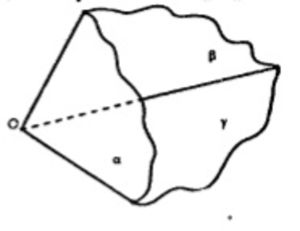
Пусть a не параллельна b, тогда a пересекается с b в некоторой точке K.
K ∈ γ, K ∈ α.
Тогда плоскость γ пересекается с плоскостью α не только по прямой c, но еще по второй прямой, проходящей через K.
То есть точка K ∈ c. Получили, что, либо плоскости имеют общую точку K, либо наше допущение неверно, то есть a || b. Если a || b, то a || α => a не пересекается с c, но лежит с ней в одной плоскости γ. Тогда по определению a || c || b.
В случае, когда плоскости имеют общую точку, они попарно пересекаются, образуя фигуру, называемую трехгранным углом
K ∈ γ, K ∈ α.
Тогда плоскость γ пересекается с плоскостью α не только по прямой c, но еще по второй прямой, проходящей через K.
То есть точка K ∈ c. Получили, что, либо плоскости имеют общую точку K, либо наше допущение неверно, то есть a || b. Если a || b, то a || α => a не пересекается с c, но лежит с ней в одной плоскости γ. Тогда по определению a || c || b.
В случае, когда плоскости имеют общую точку, они попарно пересекаются, образуя фигуру, называемую трехгранным углом

