Задание
Развернуть задание
Докажите, что середины сторон пространственного четырехугольника являются вершинами параллелограмма.
Развернуть задание
Новое решение
Решение
Соединим все вершины пространственного четырехугольника.
HE – средняя линия ∆BAD, HE || BD, GF – средняя линия ∆BCD, GF || BD.
Значит, HE || GF.
GH – средняя линия ∆ABC, GH || AC
EF – средняя линия ∆ADC, EF || AC
отсюда EF || GH
4-угольник, у которого противоположные стороны попарно параллельны, называется параллелограммом. Значит EFGH – параллелограмм.
HE – средняя линия ∆BAD, HE || BD, GF – средняя линия ∆BCD, GF || BD.
Значит, HE || GF.
GH – средняя линия ∆ABC, GH || AC
EF – средняя линия ∆ADC, EF || AC
отсюда EF || GH
4-угольник, у которого противоположные стороны попарно параллельны, называется параллелограммом. Значит EFGH – параллелограмм.
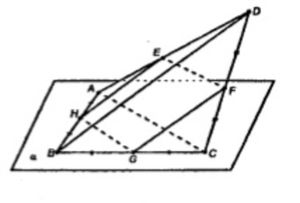
Соединим все вершины пространственного четырехугольника.
HE – средняя линия ∆BAD, HE || BD, GF – средняя линия ∆BCD, GF || BD.
Значит, HE || GF.
GH – средняя линия ∆ABC, GH || AC
EF – средняя линия ∆ADC, EF || AC
отсюда EF || GH
4-угольник, у которого противоположные стороны попарно параллельны, называется параллелограммом. Значит EFGH – параллелограмм.
HE – средняя линия ∆BAD, HE || BD, GF – средняя линия ∆BCD, GF || BD.
Значит, HE || GF.
GH – средняя линия ∆ABC, GH || AC
EF – средняя линия ∆ADC, EF || AC
отсюда EF || GH
4-угольник, у которого противоположные стороны попарно параллельны, называется параллелограммом. Значит EFGH – параллелограмм.
