Задание
Развернуть задание
Прямая m параллельна диагонали BD ромба ABCD и не лежит в плоскости ромба. Докажите, что: а) m и AC – скрещивающиеся прямые – и найдите угол между ними.
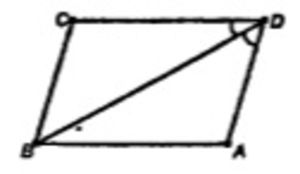
б) m и AD – скрещивающиеся прямые – и найдите угол между ними, если угол ABC = 128˚
б) m и AD – скрещивающиеся прямые – и найдите угол между ними, если угол ABC = 128˚
Развернуть задание
Новое решение
Решение
m || BD, BD лежит в α.
AC пересекает BD, т.е. m и AC скрещиваются.
AD пересекает BD, т.е. m и AD скрещиваются.
Угол между m и AC – равен углу между BD, параллельной m и AC
Угол между m и AC равен 90˚ в силу перпендикулярности диагоналей ромба.
Угол между m и AD – равен углу между BD, параллельной m и AD
BD – биссектриса (т.к. ABCD – ромб)
∠BDA = 1/2 ∠ADC = 128˚/2 = 64˚
AC пересекает BD, т.е. m и AC скрещиваются.
AD пересекает BD, т.е. m и AD скрещиваются.
Угол между m и AC – равен углу между BD, параллельной m и AC
Угол между m и AC равен 90˚ в силу перпендикулярности диагоналей ромба.
Угол между m и AD – равен углу между BD, параллельной m и AD
BD – биссектриса (т.к. ABCD – ромб)
∠BDA = 1/2 ∠ADC = 128˚/2 = 64˚
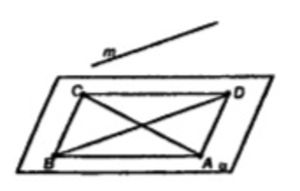
m || BD, BD лежит в α.
AC пересекает BD, т.е. m и AC скрещиваются.
AD пересекает BD, т.е. m и AD скрещиваются.
Угол между m и AC – равен углу между BD, параллельной m и AC
Угол между m и AC равен 90˚ в силу перпендикулярности диагоналей ромба.
Угол между m и AD – равен углу между BD, параллельной m и AD
BD – биссектриса (т.к. ABCD – ромб)
∠BDA = 1/2 ∠ADC = 128˚/2 = 64˚
AC пересекает BD, т.е. m и AC скрещиваются.
AD пересекает BD, т.е. m и AD скрещиваются.
Угол между m и AC – равен углу между BD, параллельной m и AC
Угол между m и AC равен 90˚ в силу перпендикулярности диагоналей ромба.
Угол между m и AD – равен углу между BD, параллельной m и AD
BD – биссектриса (т.к. ABCD – ромб)
∠BDA = 1/2 ∠ADC = 128˚/2 = 64˚

