Задание
Развернуть задание
В пространственном четырехугольнике ABCD стороны AB и CD равны. Докажите, что прямые AB и CD образуют равные углы с прямой, проходящей через середины отрезков BC и AD.
Развернуть задание
Новое решение
Решение
Соединим точки D и B, A и C.
Проведем в α KL || AB, а в плоскости BDC KN || DC.
Соединив точки N и M, точки L и M, рассмотрим MNKL.
В ∆ABC: LK || AB, BK = KC => LK – средняя линия в ∆ABC;
LK = AB/2
В ∆BDC: KN || DC, K – середина BC, поэтому KN – средняя линия в ∆BDC.
В ∆ADB: т. M – середина AD, т. N – середина BD, поэтому MN – средняя линия в ∆ADB;
MN || AB, MN = AB/2.
В ∆ADC: AM = MD, AL = LC => ML – средняя линия в ∆ADC.
ML = DC/2, ML || DC.
Значит LK = MN = DC/2
Из условия, AB = DC, значит, LK = MN = KN = ML; ML || NK и MN || LK.
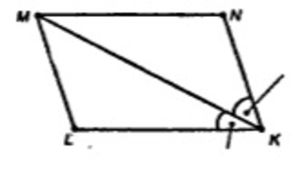
4-угольник MNKL – ромб, MK – диагональ, а в ромбе и биссектриса. Но углы NKM и LKM – искомые
Проведем в α KL || AB, а в плоскости BDC KN || DC.
Соединив точки N и M, точки L и M, рассмотрим MNKL.
В ∆ABC: LK || AB, BK = KC => LK – средняя линия в ∆ABC;
LK = AB/2
В ∆BDC: KN || DC, K – середина BC, поэтому KN – средняя линия в ∆BDC.
В ∆ADB: т. M – середина AD, т. N – середина BD, поэтому MN – средняя линия в ∆ADB;
MN || AB, MN = AB/2.
В ∆ADC: AM = MD, AL = LC => ML – средняя линия в ∆ADC.
ML = DC/2, ML || DC.
Значит LK = MN = DC/2
Из условия, AB = DC, значит, LK = MN = KN = ML; ML || NK и MN || LK.
4-угольник MNKL – ромб, MK – диагональ, а в ромбе и биссектриса. Но углы NKM и LKM – искомые
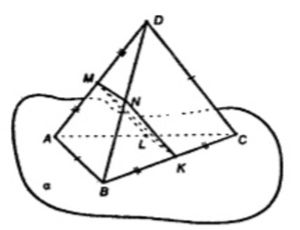
Соединим точки D и B, A и C.
Проведем в α KL || AB, а в плоскости BDC KN || DC.
Соединив точки N и M, точки L и M, рассмотрим MNKL.
В ∆ABC: LK || AB, BK = KC => LK – средняя линия в ∆ABC;
LK = AB/2
В ∆BDC: KN || DC, K – середина BC, поэтому KN – средняя линия в ∆BDC.
В ∆ADB: т. M – середина AD, т. N – середина BD, поэтому MN – средняя линия в ∆ADB;
MN || AB, MN = AB/2.
В ∆ADC: AM = MD, AL = LC => ML – средняя линия в ∆ADC.
ML = DC/2, ML || DC.
Значит LK = MN = DC/2
Из условия, AB = DC, значит, LK = MN = KN = ML; ML || NK и MN || LK.
4-угольник MNKL – ромб, MK – диагональ, а в ромбе и биссектриса. Но углы NKM и LKM – искомые
Проведем в α KL || AB, а в плоскости BDC KN || DC.
Соединив точки N и M, точки L и M, рассмотрим MNKL.
В ∆ABC: LK || AB, BK = KC => LK – средняя линия в ∆ABC;
LK = AB/2
В ∆BDC: KN || DC, K – середина BC, поэтому KN – средняя линия в ∆BDC.
В ∆ADB: т. M – середина AD, т. N – середина BD, поэтому MN – средняя линия в ∆ADB;
MN || AB, MN = AB/2.
В ∆ADC: AM = MD, AL = LC => ML – средняя линия в ∆ADC.
ML = DC/2, ML || DC.
Значит LK = MN = DC/2
Из условия, AB = DC, значит, LK = MN = KN = ML; ML || NK и MN || LK.
4-угольник MNKL – ромб, MK – диагональ, а в ромбе и биссектриса. Но углы NKM и LKM – искомые

