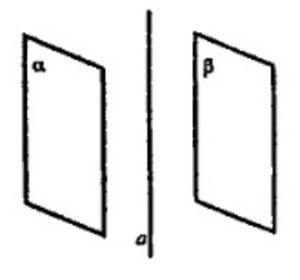
Предположим, что наша прямая а не параллельна второй плоскости. Если прямая не параллельна плоскости, значит она пересекает её, то есть прямая а пересекает β. Но так как плоскости α и β параллельные, то из нашего предположения о пересечении прямой а плоскости β следует, что прямая а пересекает плоскость α. Но по условию это не так, ведь a || α. Следовательно наше предположение неверно - a не пересекает плоскость β. В данном случае остаются два варианта - или a || β или a лежит в β.