Задание
Развернуть задание
Скорость рейсового трамвая новой конструкции на 5 км/ч больше, чем скорость прежнего трамвая, поэтому он проходит маршрут в 20 км на 12 минут быстрее, чем трамвай старой конструкции. За какое время новый трамвай проходит этот маршрут?
Развернуть задание
Новое решение
Решение
Обозначим V_ст – скорость старого трамвая. V_н – скорость нового.
t_ст – время за которое старый трамвай проходит маршрут
t_н – время за которое новый трамвай проходит маршрут
S = V/t =>
t_ст = S/ V_ст
t_н = S/V_н
По условию:
t_ст – время за которое старый трамвай проходит маршрут
t_н – время за которое новый трамвай проходит маршрут
S = V/t =>
t_ст = S/ V_ст
t_н = S/V_н
По условию:
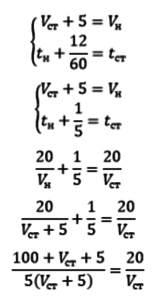
V_ст * (100 + V_ст + 5) = 100(V_ст + 5)
V_ст ^ 2 + 5*V_ст – 500 = 0
D = 25 +4*500 = 2025
Отрицательной скорости быть не может, так что:
V_ст = (-5 + 45)/2 = 20 км/ч
V_н = 20 + 5 = 25 км/ч
Тогда t_н = 20/V_н = 20/25 = 0.8 часа = 0.8 * 60 = 48 мин
Ответ: 48 мин
V_ст ^ 2 + 5*V_ст – 500 = 0
D = 25 +4*500 = 2025
Отрицательной скорости быть не может, так что:
V_ст = (-5 + 45)/2 = 20 км/ч
V_н = 20 + 5 = 25 км/ч
Тогда t_н = 20/V_н = 20/25 = 0.8 часа = 0.8 * 60 = 48 мин
Ответ: 48 мин
Обозначим V_ст – скорость старого трамвая. V_н – скорость нового.
t_ст – время за которое старый трамвай проходит маршрут
t_н – время за которое новый трамвай проходит маршрут
S = V/t =>
t_ст = S/ V_ст
t_н = S/V_н
По условию:
t_ст – время за которое старый трамвай проходит маршрут
t_н – время за которое новый трамвай проходит маршрут
S = V/t =>
t_ст = S/ V_ст
t_н = S/V_н
По условию:
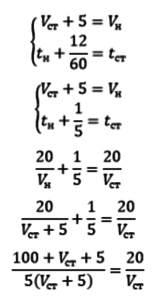
V_ст * (100 + V_ст + 5) = 100(V_ст + 5)
V_ст ^ 2 + 5*V_ст – 500 = 0
D = 25 +4*500 = 2025
Отрицательной скорости быть не может, так что:
V_ст = (-5 + 45)/2 = 20 км/ч
V_н = 20 + 5 = 25 км/ч
Тогда t_н = 20/V_н = 20/25 = 0.8 часа = 0.8 * 60 = 48 мин
Ответ: 48 мин
V_ст ^ 2 + 5*V_ст – 500 = 0
D = 25 +4*500 = 2025
Отрицательной скорости быть не может, так что:
V_ст = (-5 + 45)/2 = 20 км/ч
V_н = 20 + 5 = 25 км/ч
Тогда t_н = 20/V_н = 20/25 = 0.8 часа = 0.8 * 60 = 48 мин
Ответ: 48 мин