Задание
Развернуть задание
Пешеход и велосипедист отправились одновременно навстречу друг другу из разных городов, расстояние между которыми 40 км. Велосипедист проехал мимо пешехода через 2 часа после отправления и на весь путь затратил на 7,5 ч меньше, чем пешеход. Найти скорость движения каждого, считая, что пешеход и велосипедист двигались всё время с постоянными скоростями.
Развернуть задание
Новое решение
Решение
Пусть скорость велосипедиста – x км/ч, пешехода – y км/ч. Тогда:
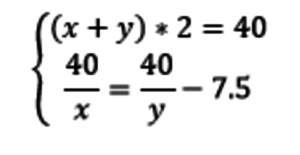
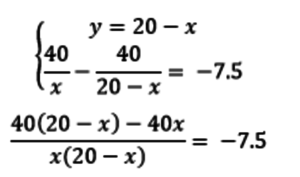
800 – 40x – 40x = -7.5x(20 – x)
800 – 80x +150x – 7.5x^2 = 0
7.5x^2 – 70x – 800 = 0
D = 4900 + 4 * 7.5 * 800 = 28900
x = (70 + 170)/15 = 16 км/ч
Тогда y = 20 – 16 = 4 км/ч
Ответ: 4 км/ч, 16 км/ч
800 – 80x +150x – 7.5x^2 = 0
7.5x^2 – 70x – 800 = 0
D = 4900 + 4 * 7.5 * 800 = 28900
x = (70 + 170)/15 = 16 км/ч
Тогда y = 20 – 16 = 4 км/ч
Ответ: 4 км/ч, 16 км/ч
Пусть скорость велосипедиста – x км/ч, пешехода – y км/ч. Тогда:
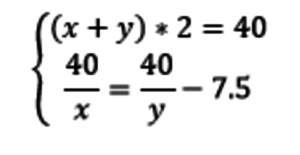
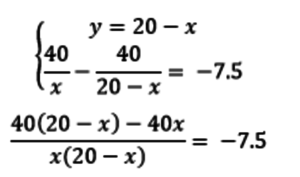
800 – 40x – 40x = -7.5x(20 – x)
800 – 80x +150x – 7.5x^2 = 0
7.5x^2 – 70x – 800 = 0
D = 4900 + 4 * 7.5 * 800 = 28900
x = (70 + 170)/15 = 16 км/ч
Тогда y = 20 – 16 = 4 км/ч
Ответ: 4 км/ч, 16 км/ч
800 – 80x +150x – 7.5x^2 = 0
7.5x^2 – 70x – 800 = 0
D = 4900 + 4 * 7.5 * 800 = 28900
x = (70 + 170)/15 = 16 км/ч
Тогда y = 20 – 16 = 4 км/ч
Ответ: 4 км/ч, 16 км/ч