Задание
Развернуть задание
Докажите, что если одна из граней вписанной в цилиндр треугольной призмы проходит через ось цилиндра, то две другие грани взаимно перпендикулярны.
Развернуть задание
Новое решение
Решение
В основании лежит окружность, в которой АВ – диаметр, ∠ACB – вписанный, он опирается на диаметр, значит, он равен 180^0 : 2 = 90^0. BC ⊥ СС_1, образующая СС_1 перпендикулярна основанию, ВС ⊥ плоскости ACC_1.
Значит, плоскость АА_1С_1С перпендикулярна плоскости ВСС_1В_1 (по признаку перпендикулярности двух плоскостей).
Значит, плоскость АА_1С_1С перпендикулярна плоскости ВСС_1В_1 (по признаку перпендикулярности двух плоскостей).
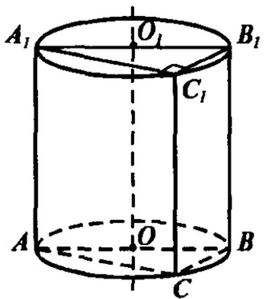
В основании лежит окружность, в которой АВ – диаметр, ∠ACB – вписанный, он опирается на диаметр, значит, он равен 180^0 : 2 = 90^0. BC ⊥ СС_1, образующая СС_1 перпендикулярна основанию, ВС ⊥ плоскости ACC_1.
Значит, плоскость АА_1С_1С перпендикулярна плоскости ВСС_1В_1 (по признаку перпендикулярности двух плоскостей).
Значит, плоскость АА_1С_1С перпендикулярна плоскости ВСС_1В_1 (по признаку перпендикулярности двух плоскостей).
