Задание
Развернуть задание
В конус высотой 12 см вписана пирамида, основанием которой является прямоугольник со сторонами 6 см и 8 см. Найдите отношение площадей полных поверхностей пирамиды и конуса.
Развернуть задание
Новое решение
Решение
Рассмотрим основание конуса. ОА = ОВ = r. Ребра пирамиды равны образующим конуса и лежат на поверхности конуса.
BD – диаметр окружности, BD = 2r. Найдём также BD из прямоугольного треугольника АВD. По т. Пифагора имеем: BD = sqrt(8^2 + 6^2) = sqrt(100) = 10 см
BD = 10 см = 2r, значит, r = 5 см
Будем искать площадь полной поверхности конуса.
S_осн = πr^2 = 25π (см^2)
Рассмотрим прямоугольный треугольник SOA. По т. Пифагора имеем:
SA = sqrt(SO^2 + OA^2) = sqrt(12^2 + 5^2) = sqrt(169) = 13 (см)
S_бок = πrl, где l = SA
S_бок = π*5*13 = 65π (см^2)
S_полн = S_бок + S_осн = (25 + 65)π = 90π (см^2)
S_ABCD = AB*BC = 6*8 = 48 (см^2)
Боковые грани попарно равны. Проведём ОК ⊥DA, OL⊥AB, отрезки SK и SL. По теореме о трёх перпендикулярах SK⊥DA и SL⊥AB.
OK = 1/2AB = 4 (см)
OL = 1/2BC = 3 (см)
Рассмотрим ∆SOK. Он прямоугольный. По т. Пифагора:
SK = sqrt(h^2 + OK^2) = sqrt(12^2 + 4^2) = sqrt(160) = 4*sqrt(10) (см)
S_∆ASD = 1/2SK*DA = ½*6*4*sqrt(10) = 12*sqrt(10) (см^2)
Рассмотрим ∆SOL. Он прямоугольный. По т. Пифагора:
SL = sqrt(h^2 + OL^2) = sqrt(12^2 + 3^2) = sqrt(153) = 3*sqrt(17) (см)
S_∆ASB = 1/2SL*AB = ½*8*3*sqrt(17) = 12*sqrt(17) (см^2)
S_бок = 2*( S_∆ASD + S_∆ASB) = 2*(12*sqrt(10)+ 12*sqrt(17)) = 24(sqrt(10)+ sqrt(17)) (см^2)
S_полн = S_бок + S-осн = 24(sqrt(10)+ sqrt(17)) + 48 = 24*(sqrt(10) + sqrt(17) + 2) (см^2)
Отношение площадей полных поверхностей пирамиды и конуса равно:
24*(sqrt(10) + sqrt(17) + 2) / 90π = 4*(sqrt(10) + sqrt(17) + 2) / 15π
Ответ: 4*(sqrt(10) + sqrt(17) + 2) / 15π
BD – диаметр окружности, BD = 2r. Найдём также BD из прямоугольного треугольника АВD. По т. Пифагора имеем: BD = sqrt(8^2 + 6^2) = sqrt(100) = 10 см
BD = 10 см = 2r, значит, r = 5 см
Будем искать площадь полной поверхности конуса.
S_осн = πr^2 = 25π (см^2)
Рассмотрим прямоугольный треугольник SOA. По т. Пифагора имеем:
SA = sqrt(SO^2 + OA^2) = sqrt(12^2 + 5^2) = sqrt(169) = 13 (см)
S_бок = πrl, где l = SA
S_бок = π*5*13 = 65π (см^2)
S_полн = S_бок + S_осн = (25 + 65)π = 90π (см^2)
S_ABCD = AB*BC = 6*8 = 48 (см^2)
Боковые грани попарно равны. Проведём ОК ⊥DA, OL⊥AB, отрезки SK и SL. По теореме о трёх перпендикулярах SK⊥DA и SL⊥AB.
OK = 1/2AB = 4 (см)
OL = 1/2BC = 3 (см)
Рассмотрим ∆SOK. Он прямоугольный. По т. Пифагора:
SK = sqrt(h^2 + OK^2) = sqrt(12^2 + 4^2) = sqrt(160) = 4*sqrt(10) (см)
S_∆ASD = 1/2SK*DA = ½*6*4*sqrt(10) = 12*sqrt(10) (см^2)
Рассмотрим ∆SOL. Он прямоугольный. По т. Пифагора:
SL = sqrt(h^2 + OL^2) = sqrt(12^2 + 3^2) = sqrt(153) = 3*sqrt(17) (см)
S_∆ASB = 1/2SL*AB = ½*8*3*sqrt(17) = 12*sqrt(17) (см^2)
S_бок = 2*( S_∆ASD + S_∆ASB) = 2*(12*sqrt(10)+ 12*sqrt(17)) = 24(sqrt(10)+ sqrt(17)) (см^2)
S_полн = S_бок + S-осн = 24(sqrt(10)+ sqrt(17)) + 48 = 24*(sqrt(10) + sqrt(17) + 2) (см^2)
Отношение площадей полных поверхностей пирамиды и конуса равно:
24*(sqrt(10) + sqrt(17) + 2) / 90π = 4*(sqrt(10) + sqrt(17) + 2) / 15π
Ответ: 4*(sqrt(10) + sqrt(17) + 2) / 15π
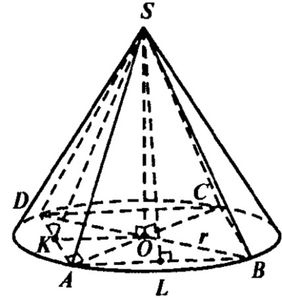
Рассмотрим основание конуса. ОА = ОВ = r. Ребра пирамиды равны образующим конуса и лежат на поверхности конуса.
BD – диаметр окружности, BD = 2r. Найдём также BD из прямоугольного треугольника АВD. По т. Пифагора имеем: BD = sqrt(8^2 + 6^2) = sqrt(100) = 10 см
BD = 10 см = 2r, значит, r = 5 см
Будем искать площадь полной поверхности конуса.
S_осн = πr^2 = 25π (см^2)
Рассмотрим прямоугольный треугольник SOA. По т. Пифагора имеем:
SA = sqrt(SO^2 + OA^2) = sqrt(12^2 + 5^2) = sqrt(169) = 13 (см)
S_бок = πrl, где l = SA
S_бок = π*5*13 = 65π (см^2)
S_полн = S_бок + S_осн = (25 + 65)π = 90π (см^2)
S_ABCD = AB*BC = 6*8 = 48 (см^2)
Боковые грани попарно равны. Проведём ОК ⊥DA, OL⊥AB, отрезки SK и SL. По теореме о трёх перпендикулярах SK⊥DA и SL⊥AB.
OK = 1/2AB = 4 (см)
OL = 1/2BC = 3 (см)
Рассмотрим ∆SOK. Он прямоугольный. По т. Пифагора:
SK = sqrt(h^2 + OK^2) = sqrt(12^2 + 4^2) = sqrt(160) = 4*sqrt(10) (см)
S_∆ASD = 1/2SK*DA = ½*6*4*sqrt(10) = 12*sqrt(10) (см^2)
Рассмотрим ∆SOL. Он прямоугольный. По т. Пифагора:
SL = sqrt(h^2 + OL^2) = sqrt(12^2 + 3^2) = sqrt(153) = 3*sqrt(17) (см)
S_∆ASB = 1/2SL*AB = ½*8*3*sqrt(17) = 12*sqrt(17) (см^2)
S_бок = 2*( S_∆ASD + S_∆ASB) = 2*(12*sqrt(10)+ 12*sqrt(17)) = 24(sqrt(10)+ sqrt(17)) (см^2)
S_полн = S_бок + S-осн = 24(sqrt(10)+ sqrt(17)) + 48 = 24*(sqrt(10) + sqrt(17) + 2) (см^2)
Отношение площадей полных поверхностей пирамиды и конуса равно:
24*(sqrt(10) + sqrt(17) + 2) / 90π = 4*(sqrt(10) + sqrt(17) + 2) / 15π
Ответ: 4*(sqrt(10) + sqrt(17) + 2) / 15π
BD – диаметр окружности, BD = 2r. Найдём также BD из прямоугольного треугольника АВD. По т. Пифагора имеем: BD = sqrt(8^2 + 6^2) = sqrt(100) = 10 см
BD = 10 см = 2r, значит, r = 5 см
Будем искать площадь полной поверхности конуса.
S_осн = πr^2 = 25π (см^2)
Рассмотрим прямоугольный треугольник SOA. По т. Пифагора имеем:
SA = sqrt(SO^2 + OA^2) = sqrt(12^2 + 5^2) = sqrt(169) = 13 (см)
S_бок = πrl, где l = SA
S_бок = π*5*13 = 65π (см^2)
S_полн = S_бок + S_осн = (25 + 65)π = 90π (см^2)
S_ABCD = AB*BC = 6*8 = 48 (см^2)
Боковые грани попарно равны. Проведём ОК ⊥DA, OL⊥AB, отрезки SK и SL. По теореме о трёх перпендикулярах SK⊥DA и SL⊥AB.
OK = 1/2AB = 4 (см)
OL = 1/2BC = 3 (см)
Рассмотрим ∆SOK. Он прямоугольный. По т. Пифагора:
SK = sqrt(h^2 + OK^2) = sqrt(12^2 + 4^2) = sqrt(160) = 4*sqrt(10) (см)
S_∆ASD = 1/2SK*DA = ½*6*4*sqrt(10) = 12*sqrt(10) (см^2)
Рассмотрим ∆SOL. Он прямоугольный. По т. Пифагора:
SL = sqrt(h^2 + OL^2) = sqrt(12^2 + 3^2) = sqrt(153) = 3*sqrt(17) (см)
S_∆ASB = 1/2SL*AB = ½*8*3*sqrt(17) = 12*sqrt(17) (см^2)
S_бок = 2*( S_∆ASD + S_∆ASB) = 2*(12*sqrt(10)+ 12*sqrt(17)) = 24(sqrt(10)+ sqrt(17)) (см^2)
S_полн = S_бок + S-осн = 24(sqrt(10)+ sqrt(17)) + 48 = 24*(sqrt(10) + sqrt(17) + 2) (см^2)
Отношение площадей полных поверхностей пирамиды и конуса равно:
24*(sqrt(10) + sqrt(17) + 2) / 90π = 4*(sqrt(10) + sqrt(17) + 2) / 15π
Ответ: 4*(sqrt(10) + sqrt(17) + 2) / 15π
