Задание
Развернуть задание
В усечённый конус вписана правильная усечённая n-угольная пирамида (т.е. основания пирамиды вписаны в основания усечённого конуса). Радиусы оснований усечённого конуса равны 2 см и 5 см, а высота равна 4 см. Вычислите площадь полной поверхности пирамиды при: a) n = 3; б) n = 4; в) n = 6.
Развернуть задание
Новое решение
Решение
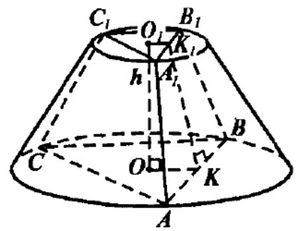
а) см. Рис.1
Пусть АС = ВС = АВ = а, тогда:
R = a/sqrt(3) (радиус окружности, описанной около большего правильного треугольника, лежащего в основании);
a = R*sqrt(3) = 5*sqrt(3) (см) (сторона этого правильного треугольника)
S_∆ABC = a^2*sqrt(3)/4 = 75*sqrt(3)/4 (см^2) (площадь этого правильного треугольника)
A1C1 = B1C1 = A1B1 = b (сторона меньшего правильного треугольника, лежащего в основании)
r = b/sqrt(3); b = r*sqrt(3) = 2*sqrt(3) (сторона меньшего правильного треугольника, лежащего в основании)
S_∆A1B1C1 = b^2*sqrt(3)/4 = 12*sqrt(3)/4 (см^2) (площадь этого правильного треугольника)
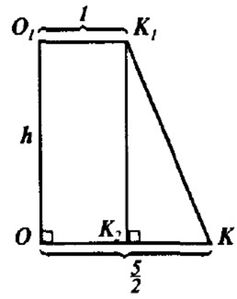
См. Рис.2
Боковые грани – равные равнобедренные трапеции. Опустим OK ⊥A1B1, OK1 ⊥AB, отрезок K1K. K1К ⊥AB (по т. о трёх перпендикулярах).
Получили, что OK, O1K1 – радиусы вписанных окружностей в ∆ABC и ∆A1B1C1 соответственно.
И, получим, OK = a/2*sqrt(3) = 5/2 (см)
O1K1 = b/2*sqrt(3) = 1 (см)
Опустим K1K2 ⊥OK. K1K2 = OK - O1K1 = 5/2 – 1 = 3/2 (см)
Из ∆K1K2K по т. Пифагора: K1K = sqrt(h^2 + 9/4) = sqrt(16 + 9/4) = sqrt(73)/2 (см)
S_бок = 3* S_ABB1O1 = 21*sqrt(3)*sqrt(73) / 4 (см^2)
Площадь полной поверхности пирамиды:
S_полн = S_бок + S_∆ABC + S_∆A1B1C1 = 21*sqrt(3)*sqrt(73) / 4 + 75*sqrt(3)/4 + 12*sqrt(3)/4 = 3*sqrt(3)*(7*sqrt(73)+29)/4;
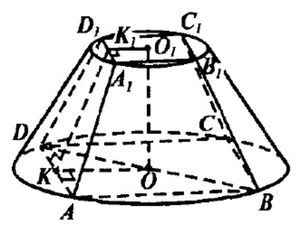
б) См. Рис.3
Пусть AB = a, тогда R = a/sqrt(2); a = R*sqrt(2) = 5*sqrt(2) (см) (сторона правильного четырёхугольника, вписанного в окружность)
S_ABCD = 5*sqrt(2) ^2 = 50 (см^2) (площадь правильного четырёхугольника)
Пусть A1B1 = b, тогда r = b/sqrt(2); b = r*sqrt(2) = 2*sqrt(2) (см) (сторона правильного четырёхугольника, вписанного в окружность).
S_A1B1C1D1 = b^2 = 8 (см^2) (площадь правильного четырёхугольника)
Боковые грани – равные равнобедренные трапеции. Опустим O1K1 ⊥D1A1, OK ⊥DA, отрезок K1K. K1К ⊥AD (по т. о трёх перпендикулярах).
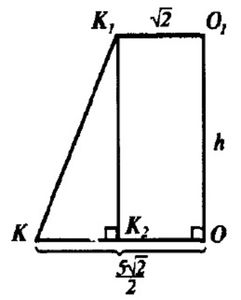
O1K1 = b/2 = sqrt(2) (см)
OK = a/2 = 5*sqrt(2)/2 (см)
K2K = OK - O1K1 = 5*sqrt(2)/2 - sqrt(2) = 3*sqrt(2) / 2(см)
См. Рис.4
Из ∆K1K2K по т. Пифагора имеем:
K1K = sqrt(h^2 + K2K1^2) = sqrt(16 + 18/4) = sqrt(82)/2 (см)
S_AA1D1D = (A1D1 +AD)*K1K/2 = (a+b)* K1K/2 = (5*sqrt(2) + 2*sqrt(2)) * sqrt(82)/2 = 7*sqrt(2)*sqrt(82)/4 (см^2)
S_бок = 4* S_AA1D1D = 7*sqrt(2)*sqrt(82) (см^2)
Площадь полной поверхности пирамиды:
S_полн = S_бок + S_ABCD + S_A1B1C1D1 = 7*sqrt(2)*sqrt(82) + 50 + 8 = 14*sqrt(41) + 58 (см^2)
в) См. Рис.5
Пусть сторона верхнего основания – b, нижнего – а. a > b. Радиус верхнего основания – r, нижнего – R. Значит, b = r, a = R.
Правильный шестиугольник включает в себя 6 равносторонних треугольников, высота каждого из них равна радиусу вписанной в шестиугольник окружности. Пусть радиус вписанной в верхний шестиугольник окружности- х, в нижний – у.
х = b*sqrt(3)/2; х = 2*sqrt(3)/2 = sqrt(3) (см)
y = a*sqrt(3)/2; y = 5*sqrt(3)/2 (см)
Площадь нижнего основания пирамиды :
6*(1/2*a*y) = 3*5*5*sqrt(3)/2 = 75*sqrt(3)/2 (см^2)
Площадь верхнего основания пирамиды :
6*(1/2*b*x) = 3*2*sqrt(3) = 6*sqrt(3) (см^2)
Боковые грани – равнобедренные трапеции. Их 6 штук. Определим высоту трапеции. В плоскости верхнего основания проводим отрезок O1K перпендикулярно к стороне шестиугольника. В плоскости нижнего основания проводим отрезок OK перпендикулярно к стороне шестиугольника. Проводим отрезок K1K
OK = y, O1K1 = x
KK2 = y – x = a*sqrt(3)/2 – b*sqrt(3)/2 = sqrt(3)/2*(a-b) = sqrt(3)/2*(R-r) = sqrt(3)/2*(5-2) = 3* sqrt(3)/2 (см)
Из ∆K1K2K по т. Пифагора:
K1K = sqrt(h^2 + (3* sqrt(3)/2)^2) = sqrt(16 + 27/4) = sqrt(91)/2 (см)
S_бок = 6*(a+b)*KK1/2 = 3*(R+r)* sqrt(91)/2 = 21* sqrt(91)/2 (см^2)
Площадь полной поверхности:
S_полн = S_бок + S_верх + S_нижн
S = 21* sqrt(91)/2 + 6*sqrt(3) + 75*sqrt(3)/2 = 3/2*(7*sqrt(91) + 29*sqrt(3)) (см^2)
Пусть АС = ВС = АВ = а, тогда:
R = a/sqrt(3) (радиус окружности, описанной около большего правильного треугольника, лежащего в основании);
a = R*sqrt(3) = 5*sqrt(3) (см) (сторона этого правильного треугольника)
S_∆ABC = a^2*sqrt(3)/4 = 75*sqrt(3)/4 (см^2) (площадь этого правильного треугольника)
A1C1 = B1C1 = A1B1 = b (сторона меньшего правильного треугольника, лежащего в основании)
r = b/sqrt(3); b = r*sqrt(3) = 2*sqrt(3) (сторона меньшего правильного треугольника, лежащего в основании)
S_∆A1B1C1 = b^2*sqrt(3)/4 = 12*sqrt(3)/4 (см^2) (площадь этого правильного треугольника)
См. Рис.2
Боковые грани – равные равнобедренные трапеции. Опустим OK ⊥A1B1, OK1 ⊥AB, отрезок K1K. K1К ⊥AB (по т. о трёх перпендикулярах).
Получили, что OK, O1K1 – радиусы вписанных окружностей в ∆ABC и ∆A1B1C1 соответственно.
И, получим, OK = a/2*sqrt(3) = 5/2 (см)
O1K1 = b/2*sqrt(3) = 1 (см)
Опустим K1K2 ⊥OK. K1K2 = OK - O1K1 = 5/2 – 1 = 3/2 (см)
Из ∆K1K2K по т. Пифагора: K1K = sqrt(h^2 + 9/4) = sqrt(16 + 9/4) = sqrt(73)/2 (см)
S_бок = 3* S_ABB1O1 = 21*sqrt(3)*sqrt(73) / 4 (см^2)
Площадь полной поверхности пирамиды:
S_полн = S_бок + S_∆ABC + S_∆A1B1C1 = 21*sqrt(3)*sqrt(73) / 4 + 75*sqrt(3)/4 + 12*sqrt(3)/4 = 3*sqrt(3)*(7*sqrt(73)+29)/4;
б) См. Рис.3
Пусть AB = a, тогда R = a/sqrt(2); a = R*sqrt(2) = 5*sqrt(2) (см) (сторона правильного четырёхугольника, вписанного в окружность)
S_ABCD = 5*sqrt(2) ^2 = 50 (см^2) (площадь правильного четырёхугольника)
Пусть A1B1 = b, тогда r = b/sqrt(2); b = r*sqrt(2) = 2*sqrt(2) (см) (сторона правильного четырёхугольника, вписанного в окружность).
S_A1B1C1D1 = b^2 = 8 (см^2) (площадь правильного четырёхугольника)
Боковые грани – равные равнобедренные трапеции. Опустим O1K1 ⊥D1A1, OK ⊥DA, отрезок K1K. K1К ⊥AD (по т. о трёх перпендикулярах).
O1K1 = b/2 = sqrt(2) (см)
OK = a/2 = 5*sqrt(2)/2 (см)
K2K = OK - O1K1 = 5*sqrt(2)/2 - sqrt(2) = 3*sqrt(2) / 2(см)
См. Рис.4
Из ∆K1K2K по т. Пифагора имеем:
K1K = sqrt(h^2 + K2K1^2) = sqrt(16 + 18/4) = sqrt(82)/2 (см)
S_AA1D1D = (A1D1 +AD)*K1K/2 = (a+b)* K1K/2 = (5*sqrt(2) + 2*sqrt(2)) * sqrt(82)/2 = 7*sqrt(2)*sqrt(82)/4 (см^2)
S_бок = 4* S_AA1D1D = 7*sqrt(2)*sqrt(82) (см^2)
Площадь полной поверхности пирамиды:
S_полн = S_бок + S_ABCD + S_A1B1C1D1 = 7*sqrt(2)*sqrt(82) + 50 + 8 = 14*sqrt(41) + 58 (см^2)
в) См. Рис.5
Пусть сторона верхнего основания – b, нижнего – а. a > b. Радиус верхнего основания – r, нижнего – R. Значит, b = r, a = R.
Правильный шестиугольник включает в себя 6 равносторонних треугольников, высота каждого из них равна радиусу вписанной в шестиугольник окружности. Пусть радиус вписанной в верхний шестиугольник окружности- х, в нижний – у.
х = b*sqrt(3)/2; х = 2*sqrt(3)/2 = sqrt(3) (см)
y = a*sqrt(3)/2; y = 5*sqrt(3)/2 (см)
Площадь нижнего основания пирамиды :
6*(1/2*a*y) = 3*5*5*sqrt(3)/2 = 75*sqrt(3)/2 (см^2)
Площадь верхнего основания пирамиды :
6*(1/2*b*x) = 3*2*sqrt(3) = 6*sqrt(3) (см^2)
Боковые грани – равнобедренные трапеции. Их 6 штук. Определим высоту трапеции. В плоскости верхнего основания проводим отрезок O1K перпендикулярно к стороне шестиугольника. В плоскости нижнего основания проводим отрезок OK перпендикулярно к стороне шестиугольника. Проводим отрезок K1K
OK = y, O1K1 = x
KK2 = y – x = a*sqrt(3)/2 – b*sqrt(3)/2 = sqrt(3)/2*(a-b) = sqrt(3)/2*(R-r) = sqrt(3)/2*(5-2) = 3* sqrt(3)/2 (см)
Из ∆K1K2K по т. Пифагора:
K1K = sqrt(h^2 + (3* sqrt(3)/2)^2) = sqrt(16 + 27/4) = sqrt(91)/2 (см)
S_бок = 6*(a+b)*KK1/2 = 3*(R+r)* sqrt(91)/2 = 21* sqrt(91)/2 (см^2)
Площадь полной поверхности:
S_полн = S_бок + S_верх + S_нижн
S = 21* sqrt(91)/2 + 6*sqrt(3) + 75*sqrt(3)/2 = 3/2*(7*sqrt(91) + 29*sqrt(3)) (см^2)
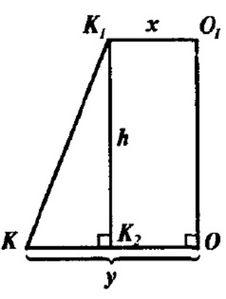
а) см. Рис.1
Пусть АС = ВС = АВ = а, тогда:
R = a/sqrt(3) (радиус окружности, описанной около большего правильного треугольника, лежащего в основании);
a = R*sqrt(3) = 5*sqrt(3) (см) (сторона этого правильного треугольника)
S_∆ABC = a^2*sqrt(3)/4 = 75*sqrt(3)/4 (см^2) (площадь этого правильного треугольника)
A1C1 = B1C1 = A1B1 = b (сторона меньшего правильного треугольника, лежащего в основании)
r = b/sqrt(3); b = r*sqrt(3) = 2*sqrt(3) (сторона меньшего правильного треугольника, лежащего в основании)
S_∆A1B1C1 = b^2*sqrt(3)/4 = 12*sqrt(3)/4 (см^2) (площадь этого правильного треугольника)
См. Рис.2
Боковые грани – равные равнобедренные трапеции. Опустим OK ⊥A1B1, OK1 ⊥AB, отрезок K1K. K1К ⊥AB (по т. о трёх перпендикулярах).
Получили, что OK, O1K1 – радиусы вписанных окружностей в ∆ABC и ∆A1B1C1 соответственно.
И, получим, OK = a/2*sqrt(3) = 5/2 (см)
O1K1 = b/2*sqrt(3) = 1 (см)
Опустим K1K2 ⊥OK. K1K2 = OK - O1K1 = 5/2 – 1 = 3/2 (см)
Из ∆K1K2K по т. Пифагора: K1K = sqrt(h^2 + 9/4) = sqrt(16 + 9/4) = sqrt(73)/2 (см)
S_бок = 3* S_ABB1O1 = 21*sqrt(3)*sqrt(73) / 4 (см^2)
Площадь полной поверхности пирамиды:
S_полн = S_бок + S_∆ABC + S_∆A1B1C1 = 21*sqrt(3)*sqrt(73) / 4 + 75*sqrt(3)/4 + 12*sqrt(3)/4 = 3*sqrt(3)*(7*sqrt(73)+29)/4;
б) См. Рис.3
Пусть AB = a, тогда R = a/sqrt(2); a = R*sqrt(2) = 5*sqrt(2) (см) (сторона правильного четырёхугольника, вписанного в окружность)
S_ABCD = 5*sqrt(2) ^2 = 50 (см^2) (площадь правильного четырёхугольника)
Пусть A1B1 = b, тогда r = b/sqrt(2); b = r*sqrt(2) = 2*sqrt(2) (см) (сторона правильного четырёхугольника, вписанного в окружность).
S_A1B1C1D1 = b^2 = 8 (см^2) (площадь правильного четырёхугольника)
Боковые грани – равные равнобедренные трапеции. Опустим O1K1 ⊥D1A1, OK ⊥DA, отрезок K1K. K1К ⊥AD (по т. о трёх перпендикулярах).
O1K1 = b/2 = sqrt(2) (см)
OK = a/2 = 5*sqrt(2)/2 (см)
K2K = OK - O1K1 = 5*sqrt(2)/2 - sqrt(2) = 3*sqrt(2) / 2(см)
См. Рис.4
Из ∆K1K2K по т. Пифагора имеем:
K1K = sqrt(h^2 + K2K1^2) = sqrt(16 + 18/4) = sqrt(82)/2 (см)
S_AA1D1D = (A1D1 +AD)*K1K/2 = (a+b)* K1K/2 = (5*sqrt(2) + 2*sqrt(2)) * sqrt(82)/2 = 7*sqrt(2)*sqrt(82)/4 (см^2)
S_бок = 4* S_AA1D1D = 7*sqrt(2)*sqrt(82) (см^2)
Площадь полной поверхности пирамиды:
S_полн = S_бок + S_ABCD + S_A1B1C1D1 = 7*sqrt(2)*sqrt(82) + 50 + 8 = 14*sqrt(41) + 58 (см^2)
в) См. Рис.5
Пусть сторона верхнего основания – b, нижнего – а. a > b. Радиус верхнего основания – r, нижнего – R. Значит, b = r, a = R.
Правильный шестиугольник включает в себя 6 равносторонних треугольников, высота каждого из них равна радиусу вписанной в шестиугольник окружности. Пусть радиус вписанной в верхний шестиугольник окружности- х, в нижний – у.
х = b*sqrt(3)/2; х = 2*sqrt(3)/2 = sqrt(3) (см)
y = a*sqrt(3)/2; y = 5*sqrt(3)/2 (см)
Площадь нижнего основания пирамиды :
6*(1/2*a*y) = 3*5*5*sqrt(3)/2 = 75*sqrt(3)/2 (см^2)
Площадь верхнего основания пирамиды :
6*(1/2*b*x) = 3*2*sqrt(3) = 6*sqrt(3) (см^2)
Боковые грани – равнобедренные трапеции. Их 6 штук. Определим высоту трапеции. В плоскости верхнего основания проводим отрезок O1K перпендикулярно к стороне шестиугольника. В плоскости нижнего основания проводим отрезок OK перпендикулярно к стороне шестиугольника. Проводим отрезок K1K
OK = y, O1K1 = x
KK2 = y – x = a*sqrt(3)/2 – b*sqrt(3)/2 = sqrt(3)/2*(a-b) = sqrt(3)/2*(R-r) = sqrt(3)/2*(5-2) = 3* sqrt(3)/2 (см)
Из ∆K1K2K по т. Пифагора:
K1K = sqrt(h^2 + (3* sqrt(3)/2)^2) = sqrt(16 + 27/4) = sqrt(91)/2 (см)
S_бок = 6*(a+b)*KK1/2 = 3*(R+r)* sqrt(91)/2 = 21* sqrt(91)/2 (см^2)
Площадь полной поверхности:
S_полн = S_бок + S_верх + S_нижн
S = 21* sqrt(91)/2 + 6*sqrt(3) + 75*sqrt(3)/2 = 3/2*(7*sqrt(91) + 29*sqrt(3)) (см^2)
Пусть АС = ВС = АВ = а, тогда:
R = a/sqrt(3) (радиус окружности, описанной около большего правильного треугольника, лежащего в основании);
a = R*sqrt(3) = 5*sqrt(3) (см) (сторона этого правильного треугольника)
S_∆ABC = a^2*sqrt(3)/4 = 75*sqrt(3)/4 (см^2) (площадь этого правильного треугольника)
A1C1 = B1C1 = A1B1 = b (сторона меньшего правильного треугольника, лежащего в основании)
r = b/sqrt(3); b = r*sqrt(3) = 2*sqrt(3) (сторона меньшего правильного треугольника, лежащего в основании)
S_∆A1B1C1 = b^2*sqrt(3)/4 = 12*sqrt(3)/4 (см^2) (площадь этого правильного треугольника)
См. Рис.2
Боковые грани – равные равнобедренные трапеции. Опустим OK ⊥A1B1, OK1 ⊥AB, отрезок K1K. K1К ⊥AB (по т. о трёх перпендикулярах).
Получили, что OK, O1K1 – радиусы вписанных окружностей в ∆ABC и ∆A1B1C1 соответственно.
И, получим, OK = a/2*sqrt(3) = 5/2 (см)
O1K1 = b/2*sqrt(3) = 1 (см)
Опустим K1K2 ⊥OK. K1K2 = OK - O1K1 = 5/2 – 1 = 3/2 (см)
Из ∆K1K2K по т. Пифагора: K1K = sqrt(h^2 + 9/4) = sqrt(16 + 9/4) = sqrt(73)/2 (см)
S_бок = 3* S_ABB1O1 = 21*sqrt(3)*sqrt(73) / 4 (см^2)
Площадь полной поверхности пирамиды:
S_полн = S_бок + S_∆ABC + S_∆A1B1C1 = 21*sqrt(3)*sqrt(73) / 4 + 75*sqrt(3)/4 + 12*sqrt(3)/4 = 3*sqrt(3)*(7*sqrt(73)+29)/4;
б) См. Рис.3
Пусть AB = a, тогда R = a/sqrt(2); a = R*sqrt(2) = 5*sqrt(2) (см) (сторона правильного четырёхугольника, вписанного в окружность)
S_ABCD = 5*sqrt(2) ^2 = 50 (см^2) (площадь правильного четырёхугольника)
Пусть A1B1 = b, тогда r = b/sqrt(2); b = r*sqrt(2) = 2*sqrt(2) (см) (сторона правильного четырёхугольника, вписанного в окружность).
S_A1B1C1D1 = b^2 = 8 (см^2) (площадь правильного четырёхугольника)
Боковые грани – равные равнобедренные трапеции. Опустим O1K1 ⊥D1A1, OK ⊥DA, отрезок K1K. K1К ⊥AD (по т. о трёх перпендикулярах).
O1K1 = b/2 = sqrt(2) (см)
OK = a/2 = 5*sqrt(2)/2 (см)
K2K = OK - O1K1 = 5*sqrt(2)/2 - sqrt(2) = 3*sqrt(2) / 2(см)
См. Рис.4
Из ∆K1K2K по т. Пифагора имеем:
K1K = sqrt(h^2 + K2K1^2) = sqrt(16 + 18/4) = sqrt(82)/2 (см)
S_AA1D1D = (A1D1 +AD)*K1K/2 = (a+b)* K1K/2 = (5*sqrt(2) + 2*sqrt(2)) * sqrt(82)/2 = 7*sqrt(2)*sqrt(82)/4 (см^2)
S_бок = 4* S_AA1D1D = 7*sqrt(2)*sqrt(82) (см^2)
Площадь полной поверхности пирамиды:
S_полн = S_бок + S_ABCD + S_A1B1C1D1 = 7*sqrt(2)*sqrt(82) + 50 + 8 = 14*sqrt(41) + 58 (см^2)
в) См. Рис.5
Пусть сторона верхнего основания – b, нижнего – а. a > b. Радиус верхнего основания – r, нижнего – R. Значит, b = r, a = R.
Правильный шестиугольник включает в себя 6 равносторонних треугольников, высота каждого из них равна радиусу вписанной в шестиугольник окружности. Пусть радиус вписанной в верхний шестиугольник окружности- х, в нижний – у.
х = b*sqrt(3)/2; х = 2*sqrt(3)/2 = sqrt(3) (см)
y = a*sqrt(3)/2; y = 5*sqrt(3)/2 (см)
Площадь нижнего основания пирамиды :
6*(1/2*a*y) = 3*5*5*sqrt(3)/2 = 75*sqrt(3)/2 (см^2)
Площадь верхнего основания пирамиды :
6*(1/2*b*x) = 3*2*sqrt(3) = 6*sqrt(3) (см^2)
Боковые грани – равнобедренные трапеции. Их 6 штук. Определим высоту трапеции. В плоскости верхнего основания проводим отрезок O1K перпендикулярно к стороне шестиугольника. В плоскости нижнего основания проводим отрезок OK перпендикулярно к стороне шестиугольника. Проводим отрезок K1K
OK = y, O1K1 = x
KK2 = y – x = a*sqrt(3)/2 – b*sqrt(3)/2 = sqrt(3)/2*(a-b) = sqrt(3)/2*(R-r) = sqrt(3)/2*(5-2) = 3* sqrt(3)/2 (см)
Из ∆K1K2K по т. Пифагора:
K1K = sqrt(h^2 + (3* sqrt(3)/2)^2) = sqrt(16 + 27/4) = sqrt(91)/2 (см)
S_бок = 6*(a+b)*KK1/2 = 3*(R+r)* sqrt(91)/2 = 21* sqrt(91)/2 (см^2)
Площадь полной поверхности:
S_полн = S_бок + S_верх + S_нижн
S = 21* sqrt(91)/2 + 6*sqrt(3) + 75*sqrt(3)/2 = 3/2*(7*sqrt(91) + 29*sqrt(3)) (см^2)




