Ольга «Если его умножить на 4, к произведению прибавить 8 и полученную сумму разделить
на 2, то получится 10». Обозначим за x число. Умножим на 4 ; 4x. Прибавим 8 ; 4x + 8.
Полученную сумму поделим на 2; (4x + 8)/2. И все это теперь равно 10 ; (4x + 8)/2 = 10
Задание
Развернуть задание
Докажите, что центр сферы, вписанной в правильную пирамиду, лежит на высоте этой пирамиды.
Развернуть задание
Новое решение
Решение
Будем рассматривать треугольную правильную пирамиду. SD – высота. Опустим AE⊥BC. Проведём SE. SE⊥CB (по теореме о трёх перпендикулярах).
Впишем в ∆SDE полуокружность DFG с центром в точке О, которая лежит на SD, а дуга данной полуокружности касается DE и SE. ∆SDE и полуокружность DFG будем поворачивать вокруг SD. Тогда при повороте DE будет описывать окружность, вписанную в ∆АВС, поэтому SE при вращении останется внутри пирамиды, кроме трёх положений, когда SE будет совпадать с высотой боковых граней.
Таким образом, полученная нами сфера (вращали полуокружность DFG) будет иметь единственную общую точку с каждой из боковых граней. Эта сфера касается также основания пирамиды в точке D. Центр этой сферы лежит на высоте SD.
Впишем в ∆SDE полуокружность DFG с центром в точке О, которая лежит на SD, а дуга данной полуокружности касается DE и SE. ∆SDE и полуокружность DFG будем поворачивать вокруг SD. Тогда при повороте DE будет описывать окружность, вписанную в ∆АВС, поэтому SE при вращении останется внутри пирамиды, кроме трёх положений, когда SE будет совпадать с высотой боковых граней.
Таким образом, полученная нами сфера (вращали полуокружность DFG) будет иметь единственную общую точку с каждой из боковых граней. Эта сфера касается также основания пирамиды в точке D. Центр этой сферы лежит на высоте SD.
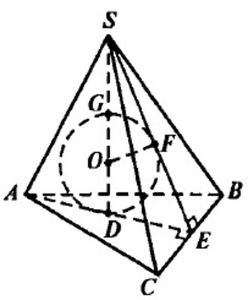
Будем рассматривать треугольную правильную пирамиду. SD – высота. Опустим AE⊥BC. Проведём SE. SE⊥CB (по теореме о трёх перпендикулярах).
Впишем в ∆SDE полуокружность DFG с центром в точке О, которая лежит на SD, а дуга данной полуокружности касается DE и SE. ∆SDE и полуокружность DFG будем поворачивать вокруг SD. Тогда при повороте DE будет описывать окружность, вписанную в ∆АВС, поэтому SE при вращении останется внутри пирамиды, кроме трёх положений, когда SE будет совпадать с высотой боковых граней.
Таким образом, полученная нами сфера (вращали полуокружность DFG) будет иметь единственную общую точку с каждой из боковых граней. Эта сфера касается также основания пирамиды в точке D. Центр этой сферы лежит на высоте SD.
Впишем в ∆SDE полуокружность DFG с центром в точке О, которая лежит на SD, а дуга данной полуокружности касается DE и SE. ∆SDE и полуокружность DFG будем поворачивать вокруг SD. Тогда при повороте DE будет описывать окружность, вписанную в ∆АВС, поэтому SE при вращении останется внутри пирамиды, кроме трёх положений, когда SE будет совпадать с высотой боковых граней.
Таким образом, полученная нами сфера (вращали полуокружность DFG) будет иметь единственную общую точку с каждой из боковых граней. Эта сфера касается также основания пирамиды в точке D. Центр этой сферы лежит на высоте SD.
