Решения
Диана


06-12-2016 20:29

0
Задания
Задание
Ира
06-12-2016
17:01
Школа

Геометрия

11 класс


11
1
0
0

Шар и сфера, их сечения

Найти площадь боковой поверхности пирамиды.

Развернуть задание
Около сферы радиуса R описана правильная четырёхугольная пирамида, плоский угол при вершине которой равен α.
а) Найдите площадь боковой поверхности пирамиды
б) Вычислите эту площадь при R = 5 см, α = 600.
Сергей Геннадиевич
Новый коммент
24-07-2017 17:41:17
Алиса
Судя по таблице удельной теплоёмкости, это может быть цинк.
22-11-2016 12:57:23
Анастасия
Дмитрий Да, перевод обязателен.
21-11-2016 19:00:39
Дмитрий
1) –Обязательно ли переводить массу мяча в СИ?
21-11-2016 18:51:12
Рогова Дарья
Условие смущает. Ладно, пусть время будет отрицательным, наблюдать можно с любого момента, но не ясно, каким моментам времени соответствуют моменты изменения скорости. Можно предположить, что первый пик где-то в районе -1,5 с, но так ли это?.. Третий пик вообще без координатной сетки не определишь. И еще: график чего именно надо построить? МОДУЛЯ скорости или ПРОЕКЦИИ скорости?
3-11-2016 00:11:19
Андрей Анатольевич
Почему картика в блоке так размыта? А при просмотре в правой части (крупно) все выглядит гораздо лучше. Как то плохо пережимается картинка.
2-11-2016 15:29:02
Андрей Анатольевич
t = 20ºC или 200 С ?
31-10-2016 20:21:46
Эдуард Блохин
Интересное задание. Пригодится.
27-10-2016 14:34:02
Развернуть задание
Новое решение
Сложность
4 3 2 1
Решение
Диана
6-12-2016 20:29:35
0
а) Проведём через точку О MN||AD, также проведём отрезки PM и PN. PN⊥DC, PM⊥AB (по т. о трех перпендикулярах). Центр сферы будет в точке пересечения биссектрис двугранных углов при основании. Но также центр сферы, вписанной в правильную пирамиду, лежит на высоте пирамиды. Значит, SN – биссектриса угла PNO. А угол PNO – линейный угол двугранного угла при основании пирамиды.

Пусть AD = a, PN = x
tg(α/2) = a/2x, откуда х = a/(2* tg(α/2) )

Пусть угол PKO = γ, 0 < γ < 900

Рассмотрим ∆PON: cosγ = ON/PN = a/2x = a/2 : a/(2* tg(α/2) ) = tg(α/2)
sinγ = sqrt(1 – cosγ^2) (используем основное тригонометрическое тождество)
sinγ = sqrt(1- tg(α/2)^2)

Рассмотрим ∆SON: tg(γ/2) = SO/ON = 2R/a
2R/a = sinγ / (1+cosγ) = sqrt(1- tg(α/2)^2) / (1+ tg(α/2)), отсюда a = 2*R*(1+ tg(α/2))/ sqrt(1- tg(α/2)^2)
x = 2*R*(1+ tg(α/2))/ sqrt(1- tg(α/2)^2) * 1/2* tg(α/2) = R*(1+ tg(α/2)) / tg(α/2)* sqrt(1- tg(α/2)^2)

S_∆DCP = ½*a*x = ½ * 2*R*(1+ tg(α/2))/ sqrt(1- tg(α/2)^2) * R*(1+ tg(α/2)) / tg(α/2)* sqrt(1- tg(α/2)^2) = R^2*(1+ tg(α/2)) / tg(α/2)* (1- tg(α/2))

S_бок = 4* S_∆DCP = 4* R^2*(1+ tg(α/2)) / tg(α/2)* (1- tg(α/2)) = 4* R^2 / tg(α/2) * (cos(α/2) + sin(α/2) ) / (cos(α/2) - sin(α/2))

cosα = (cos(α/2))^2 – (sin(α/2))^2 = (cos(α/2) + sin(α/2) ) *(cos(α/2) - sin(α/2)), отсюда
cos(α/2) + sin(α/2) = cosα / (cos(α/2) - sin(α/2))

Итак, S_бок = 4* R^2 / tg(α/2) * cosα / ((cos(α/2))^2 – (sin(α/2))^2 – 2*cos(α/2)*sin(α/2)) = 4* R^2 / tg(α/2) * cosα /(1 – sinα)

б) При R = 5 и α = 600:
S_бок = 4* R^2 / tg(α/2) * cosα /(1 – sinα) = 100/(1/sqrt(3)) * ½ / (1 – sqrt(3)/2) = 100*sqrt(3)*(2 + sqrt(3)) (см^2)

Ответ: а) S_бок = 4* R^2 / tg(α/2) * cosα /(1 – sinα); б) 100*sqrt(3)*(2 + sqrt(3)) (см^2)
Анастасия
Формула внутренней энергии газа.
26-11-2016 03:00:17
Елизавета
а что это за формула?
26-11-2016 02:40:45
KatieStark
Из таблицы удельной теплоёмкости.
25-11-2016 09:24:03
Катя
Откуда мы взяли удельную теплоёмкость меди?
25-11-2016 09:23:36
Катя
Если посмотреть со стороны математики, объём измеряется в литрах, плотность в кг/л.
Умножаем одно на другое, литры сокращаются и остаются только килограммы. Вот и масса.
25-11-2016 09:19:38
KatieStark
Почему, умножая объём на плотность, мы получаем массу?
25-11-2016 09:18:47
Дмитрий
Скорее всего, в жидком или переходило в него,
потому что температура плавления олова как раз 231.9 0 C
25-11-2016 09:13:37
KatieStark
В каком агрегатном состоянии находилось олово до охлаждения?
25-11-2016 09:12:54
Анастасия
Ну, судя по таблице теплоёмкости – да.
25-11-2016 09:06:12
KatieStark
Получается, этот металл – свинец?
25-11-2016 09:05:45
Анастасия
Елизавета потому что данная единица масштаба предоставлена в условии как единица измерения.
24-11-2016 20:11:10
Анастасия
Елизавета потому что на спутник действует земное притяжение и чем ближе к Земле, тем оно сильнее, поэтому чтобы его преодолеть, нужна большая скорость, чем на других участках.
24-11-2016 20:10:16
Анастасия
Елизавета так как траектория движения стрелки представляет собой окружность, то пройденный путь будет равен длине данной окружности, поэтому пользуемся формулой L=2пR.
24-11-2016 20:08:59
Анастасия
Елизавета потому что перемещение –это вектор , проведённый из точки-начала пути в точку- конец пути, в данном случае вектор представляет собой гипотенузу треугольника пройденного пути.
24-11-2016 20:08:01
Анастасия
Елизавета так как если опустить перпендикуляры на соответствующие оси из начала и конца данных векторов, то они совпадут, длина проекции данных векторов равна разности конца и начала проекций в соответствующий у.е., а в этих случая длина равна 0, следовательно, вектора нулевые.
24-11-2016 20:07:01
Анастасия
Елизавета начало движения засекают по крайней правой точке переднего колеса, а конец движения замеряют по левой точке заднего колеса, таким образом каждая точка колеса от пункта А до пункта Б проходит одно и тоже расстояние.
24-11-2016 20:03:33
Анастасия
Елизавета во время выполнения данной фигуры все самолеты имеют одинаковую скорость и их траектория неизменна.
24-11-2016 20:02:12
Анастасия
Елизавета так как вовремя стыковки они соединились, то есть стали одним физическим телом, то скорость их движения относительно друг друга равна 0,это аналогично столику в купе поезда: скорость столика относительно поезда равна 0.
24-11-2016 20:00:29
Анастасия
Елизавета ось колеса связана с рамой велосипеда так, что во время движения она неподвижна, но колесо прокручивается вокруг оси, каждая точка колеса зафиксирована на нём, поэтому их траектория совпадает с траекторией самого колеса, траектория которого в свою очередь-окружность.
24-11-2016 19:58:50
Анастасия
Елизавета центр колеса-центр окружности, через которую проходит ось колеса(ось, фиксирующая колесо на машине),машина перемещает во время движения вдоль дороги, следовательно ось и каждая её точка перемещаются вдоль дороги(в том числе и центр колеса),поэтому траектория центра-прямая линия.
24-11-2016 19:57:30
Диана
6-12-2016 20:29:35
0
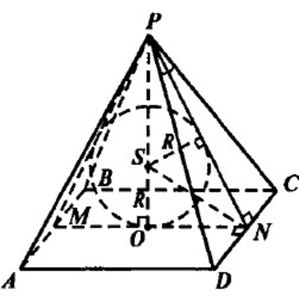
а) Проведём через точку О MN||AD, также проведём отрезки PM и PN. PN⊥DC, PM⊥AB (по т. о трех перпендикулярах). Центр сферы будет в точке пересечения биссектрис двугранных углов при основании. Но также центр сферы, вписанной в правильную пирамиду, лежит на высоте пирамиды. Значит, SN – биссектриса угла PNO. А угол PNO – линейный угол двугранного угла при основании пирамиды.

Пусть AD = a, PN = x
tg(α/2) = a/2x, откуда х = a/(2* tg(α/2) )

Пусть угол PKO = γ, 0 < γ < 900

Рассмотрим ∆PON: cosγ = ON/PN = a/2x = a/2 : a/(2* tg(α/2) ) = tg(α/2)
sinγ = sqrt(1 – cosγ^2) (используем основное тригонометрическое тождество)
sinγ = sqrt(1- tg(α/2)^2)

Рассмотрим ∆SON: tg(γ/2) = SO/ON = 2R/a
2R/a = sinγ / (1+cosγ) = sqrt(1- tg(α/2)^2) / (1+ tg(α/2)), отсюда a = 2*R*(1+ tg(α/2))/ sqrt(1- tg(α/2)^2)
x = 2*R*(1+ tg(α/2))/ sqrt(1- tg(α/2)^2) * 1/2* tg(α/2) = R*(1+ tg(α/2)) / tg(α/2)* sqrt(1- tg(α/2)^2)

S_∆DCP = ½*a*x = ½ * 2*R*(1+ tg(α/2))/ sqrt(1- tg(α/2)^2) * R*(1+ tg(α/2)) / tg(α/2)* sqrt(1- tg(α/2)^2) = R^2*(1+ tg(α/2)) / tg(α/2)* (1- tg(α/2))

S_бок = 4* S_∆DCP = 4* R^2*(1+ tg(α/2)) / tg(α/2)* (1- tg(α/2)) = 4* R^2 / tg(α/2) * (cos(α/2) + sin(α/2) ) / (cos(α/2) - sin(α/2))

cosα = (cos(α/2))^2 – (sin(α/2))^2 = (cos(α/2) + sin(α/2) ) *(cos(α/2) - sin(α/2)), отсюда
cos(α/2) + sin(α/2) = cosα / (cos(α/2) - sin(α/2))

Итак, S_бок = 4* R^2 / tg(α/2) * cosα / ((cos(α/2))^2 – (sin(α/2))^2 – 2*cos(α/2)*sin(α/2)) = 4* R^2 / tg(α/2) * cosα /(1 – sinα)

б) При R = 5 и α = 600:
S_бок = 4* R^2 / tg(α/2) * cosα /(1 – sinα) = 100/(1/sqrt(3)) * ½ / (1 – sqrt(3)/2) = 100*sqrt(3)*(2 + sqrt(3)) (см^2)

Ответ: а) S_бок = 4* R^2 / tg(α/2) * cosα /(1 – sinα); б) 100*sqrt(3)*(2 + sqrt(3)) (см^2)
Новость часа

Форма обратной связи