Даша Здесь мы использовали свойство параллелограмма (противоположные стороны
параллелограмма равны)
Задание
Развернуть задание
Докажите, что центр сферы, описанной около: а) правильной призмы, лежит в середине отрезка, соединяющего центры оснований этой призмы; б) правильной пирамиды, лежит на высоте этой пирамиды или её продолжении.
Развернуть задание
Новое решение
Решение
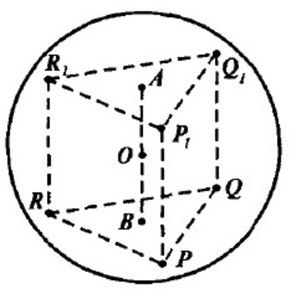
а) См. Рис.1
Пусть А и В – центры оснований. В основаниях лежат равные равносторонние треугольники. Точки, лежащие на перпендикуляре к верхнему основанию призмы, проведённом через точку В, равноудалены от вершин треугольника PQR. А все точки, которые лежат на перпендикуляре к нижнему основанию призмы, который проведён через точку А, равноудалены от вершин ∆P1Q1R1. Наша призма правильная, ∆P1Q1R1 и ∆PQR проектируются друг на друга, т.е. точка В проектируется на А и обратно. Значит, АВ перпендикулярен плоскости PQR. Значит, получается, что АВ – геометрическое место точек, равноудалённых от вершин каждого из треугольников. О – середина АВ, равноудалена от вершин ∆P1Q1R1 и ∆PQR на R – радиус описанной около призмы сферы.
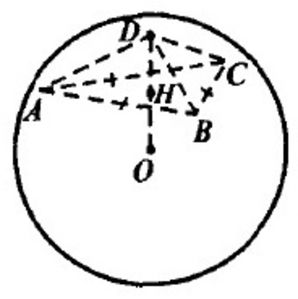
б) См. Рис.2
Опустим высоту DH, DH перпендикулярен плоскости АВС. Проведём HA, HB, HC.
∆DHA = ∆DHB = ∆DHC (по двум катетам), значит, HA = HB = HC = r, r – радиус описанной около ∆АВС окружности.
Из центра сферы (точка О) проводим отрезок OG, перпендикулярный плоскости ABC. Проведём GA, GB, GC, OA, OB, OC. ∆OGA = ∆OGB = ∆OGC (по двум катетам). Значит, GA = GB = GC = r, r – радиус описанной около ∆АВС окружности.
Но вокруг ∆АВС можно описать единственную окружность, т.е. точки H и G совпадают, D, H, O лежат на одной прямой. Значит, центр сферы О лежит на высоте пирамиды DH или на продолжении за точку Н.
Пусть А и В – центры оснований. В основаниях лежат равные равносторонние треугольники. Точки, лежащие на перпендикуляре к верхнему основанию призмы, проведённом через точку В, равноудалены от вершин треугольника PQR. А все точки, которые лежат на перпендикуляре к нижнему основанию призмы, который проведён через точку А, равноудалены от вершин ∆P1Q1R1. Наша призма правильная, ∆P1Q1R1 и ∆PQR проектируются друг на друга, т.е. точка В проектируется на А и обратно. Значит, АВ перпендикулярен плоскости PQR. Значит, получается, что АВ – геометрическое место точек, равноудалённых от вершин каждого из треугольников. О – середина АВ, равноудалена от вершин ∆P1Q1R1 и ∆PQR на R – радиус описанной около призмы сферы.
б) См. Рис.2
Опустим высоту DH, DH перпендикулярен плоскости АВС. Проведём HA, HB, HC.
∆DHA = ∆DHB = ∆DHC (по двум катетам), значит, HA = HB = HC = r, r – радиус описанной около ∆АВС окружности.
Из центра сферы (точка О) проводим отрезок OG, перпендикулярный плоскости ABC. Проведём GA, GB, GC, OA, OB, OC. ∆OGA = ∆OGB = ∆OGC (по двум катетам). Значит, GA = GB = GC = r, r – радиус описанной около ∆АВС окружности.
Но вокруг ∆АВС можно описать единственную окружность, т.е. точки H и G совпадают, D, H, O лежат на одной прямой. Значит, центр сферы О лежит на высоте пирамиды DH или на продолжении за точку Н.
а) См. Рис.1
Пусть А и В – центры оснований. В основаниях лежат равные равносторонние треугольники. Точки, лежащие на перпендикуляре к верхнему основанию призмы, проведённом через точку В, равноудалены от вершин треугольника PQR. А все точки, которые лежат на перпендикуляре к нижнему основанию призмы, который проведён через точку А, равноудалены от вершин ∆P1Q1R1. Наша призма правильная, ∆P1Q1R1 и ∆PQR проектируются друг на друга, т.е. точка В проектируется на А и обратно. Значит, АВ перпендикулярен плоскости PQR. Значит, получается, что АВ – геометрическое место точек, равноудалённых от вершин каждого из треугольников. О – середина АВ, равноудалена от вершин ∆P1Q1R1 и ∆PQR на R – радиус описанной около призмы сферы.
б) См. Рис.2
Опустим высоту DH, DH перпендикулярен плоскости АВС. Проведём HA, HB, HC.
∆DHA = ∆DHB = ∆DHC (по двум катетам), значит, HA = HB = HC = r, r – радиус описанной около ∆АВС окружности.
Из центра сферы (точка О) проводим отрезок OG, перпендикулярный плоскости ABC. Проведём GA, GB, GC, OA, OB, OC. ∆OGA = ∆OGB = ∆OGC (по двум катетам). Значит, GA = GB = GC = r, r – радиус описанной около ∆АВС окружности.
Но вокруг ∆АВС можно описать единственную окружность, т.е. точки H и G совпадают, D, H, O лежат на одной прямой. Значит, центр сферы О лежит на высоте пирамиды DH или на продолжении за точку Н.
Пусть А и В – центры оснований. В основаниях лежат равные равносторонние треугольники. Точки, лежащие на перпендикуляре к верхнему основанию призмы, проведённом через точку В, равноудалены от вершин треугольника PQR. А все точки, которые лежат на перпендикуляре к нижнему основанию призмы, который проведён через точку А, равноудалены от вершин ∆P1Q1R1. Наша призма правильная, ∆P1Q1R1 и ∆PQR проектируются друг на друга, т.е. точка В проектируется на А и обратно. Значит, АВ перпендикулярен плоскости PQR. Значит, получается, что АВ – геометрическое место точек, равноудалённых от вершин каждого из треугольников. О – середина АВ, равноудалена от вершин ∆P1Q1R1 и ∆PQR на R – радиус описанной около призмы сферы.
б) См. Рис.2
Опустим высоту DH, DH перпендикулярен плоскости АВС. Проведём HA, HB, HC.
∆DHA = ∆DHB = ∆DHC (по двум катетам), значит, HA = HB = HC = r, r – радиус описанной около ∆АВС окружности.
Из центра сферы (точка О) проводим отрезок OG, перпендикулярный плоскости ABC. Проведём GA, GB, GC, OA, OB, OC. ∆OGA = ∆OGB = ∆OGC (по двум катетам). Значит, GA = GB = GC = r, r – радиус описанной около ∆АВС окружности.
Но вокруг ∆АВС можно описать единственную окружность, т.е. точки H и G совпадают, D, H, O лежат на одной прямой. Значит, центр сферы О лежит на высоте пирамиды DH или на продолжении за точку Н.

