Задание
Развернуть задание
Докажите, что: а) около любого тетраэдра можно описать сферу; б) в любой тетраэдр можно вписать сферу.
Развернуть задание
Новое решение
Решение
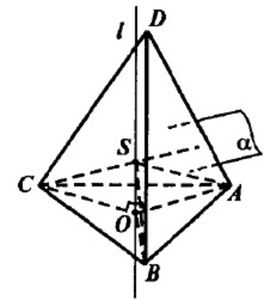
а) См. Рис.1
Будем доказывать, что через любые 4 точки, не лежащие в одной плоскости, можно провести сферу, и притом только одну. Центр сферы, описанной около тетраэдра, должен принадлежать каждой из плоскостей, проведённых через середины рёбер тетраэдра перпендикулярно к его рёбрам.
Пусть О – центр окружности, описанной около грани АВС, l – прямая, проходит через О и перпендикулярна плоскости АВС. Каждая точка l равноудалена от точек А, В, С. (ОА = ОВ = ОС = r – радиус описанной окружности). Если S лежит на l, то ∆SOA = ∆SOB = ∆SOC (по двум катетам). Значит, SA = SB = SC.
Пусть плоскость α проходит через середину DA и перпендикулярна DA. Нужно доказать, что l и α пересекаются. Предположим, что это не так, т.е. что они параллельны.
Если α ⊥AD и l || α, то AD ⊥l. Но l ⊥AB и, тогда, l ⊥ABD (по признаку перпендикулярности прямой плоскости).
Значит, через одну точку были проведены две разные плоскости, перпендикулярные к одной прямой. Наше предположение неверно, т.е. l и α пересекаются. Пусть S – их точка пересечения. Тогда SD = SA. Т.к. S лежит на l, то SA = SB = SC, и, следовательно, S равноудалена от всех вершин тетраэдра.
Обозначим через R расстояние от О до одной из вершин тетраэдра. Сфера с центром в S и радиусом R проходит через все данные точки. Из доказанного выше следует, что такая сфера может быть только одна.
Таким образом, доказали, что около любого тетраэдра можно описать сферу
б) Будем рассматривать 2 грани с общим ребром. Геометрическим местом точек, равноудалённых от обеих граней двугранного угла, будет плоскость, делящая двугранный угол пополам, или, другими словами, биссекторная плоскость этого двугранного угла. Поэтому центр сферы, вписанной в тетраэдр, равноудалён от всех граней пирамиды, он принадлежит каждой из биссекторных плоскостей, т.е. он – точка пересечения биссекторных плоскостей всех двугранных углов тетраэдра. Центр сферы, вписанной в тетраэдр, всегда находится внутри тетраэдра, т.к. все точки биссекторной плоскости расположены между гранями двугранного угла.
Таким образом, центр у вписанной сферы может быть только один. Сфера с центром в этой точке и радиусом, равным расстоянию от этой точки до плоскости какой-либо грани тетраэдра, касается всех граней тетраэдра. Значит, в любой тетраэдр можно вписать сферу и притом только одну.
Осталось лишь доказать, что биссекторные плоскости двугранных углов тетраэдра пересекаются в одной точке.
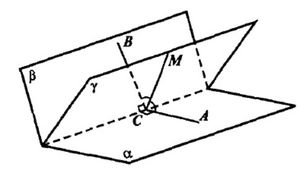
См. Рис.2
M лежит на γ. Угол АСВ – линейный угол двугранного угла между плоскостями α и β.
Пусть γ делит этот угол так, что углы ВСМ и АСМ равны, т.е. γ – биссекторная плоскость. Докажем, что биссекторные плоскости двугранных углов трёхгранного угла пересекаются по одному лучу.
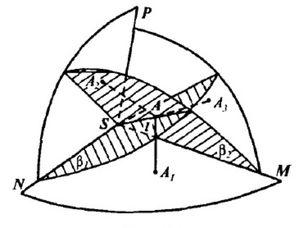
См. Рис.3
β1 и β2 – биссекторные плоскости, их пересечение – луч l, исходящий из вершины S тетраэдра. Пусть А, принадлежащая l, произвольная точка луча. Проведём перпендикуляры AA1, AA2, AA3 на грани трёхгранного угла. A принадлежит β1, поэтому АА2 = AA1; A принадлежит β2, поэтому АА3 = AA1.
Значит AA1 = AA2 = AA3, т.е. А равноудалена от плоскостей граней NSP и MSP. Значит, А находится на биссеторной плоскости двугранного угла с ребром SP. Т.к. мы выбирали А произвольно, значит, весь луч находится в биссекторной плоскости. Значит, все три биссекторные плоскости пересекаются по одному лучу, любая точка которых равноудалена.
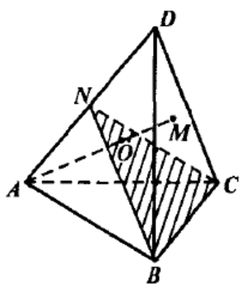
См. Рис.4
Пусть l – луч, по которому пересекаются биссекторные плоскости трёхгранного угла при вершине А, М – точка, в которой l пересекает BDC. Концы АМ принадлежат разным граням двугранного угла при ребре ВС, поэтому биссекторная плоскость этого двугранного угла пересечёт отрезок АМ в точке О. О лежит на l, поэтому она равноудалена от плоскостей ABC, ABD и ACD. Кроме этого, расстояние от О до ABC и BCD равны, т.к. О принадлежит биссекторной плоскости двугранного угла при ребре ВС. Значит, О равноудалена от всех граней тетраэдра, т.е. принадлежит всем биссекторным плоскостям двугранных углов тетраэдра. Итак, биссекторные плоскости двугранных углов тетраэдра пересекаются в одной точке.
Будем доказывать, что через любые 4 точки, не лежащие в одной плоскости, можно провести сферу, и притом только одну. Центр сферы, описанной около тетраэдра, должен принадлежать каждой из плоскостей, проведённых через середины рёбер тетраэдра перпендикулярно к его рёбрам.
Пусть О – центр окружности, описанной около грани АВС, l – прямая, проходит через О и перпендикулярна плоскости АВС. Каждая точка l равноудалена от точек А, В, С. (ОА = ОВ = ОС = r – радиус описанной окружности). Если S лежит на l, то ∆SOA = ∆SOB = ∆SOC (по двум катетам). Значит, SA = SB = SC.
Пусть плоскость α проходит через середину DA и перпендикулярна DA. Нужно доказать, что l и α пересекаются. Предположим, что это не так, т.е. что они параллельны.
Если α ⊥AD и l || α, то AD ⊥l. Но l ⊥AB и, тогда, l ⊥ABD (по признаку перпендикулярности прямой плоскости).
Значит, через одну точку были проведены две разные плоскости, перпендикулярные к одной прямой. Наше предположение неверно, т.е. l и α пересекаются. Пусть S – их точка пересечения. Тогда SD = SA. Т.к. S лежит на l, то SA = SB = SC, и, следовательно, S равноудалена от всех вершин тетраэдра.
Обозначим через R расстояние от О до одной из вершин тетраэдра. Сфера с центром в S и радиусом R проходит через все данные точки. Из доказанного выше следует, что такая сфера может быть только одна.
Таким образом, доказали, что около любого тетраэдра можно описать сферу
б) Будем рассматривать 2 грани с общим ребром. Геометрическим местом точек, равноудалённых от обеих граней двугранного угла, будет плоскость, делящая двугранный угол пополам, или, другими словами, биссекторная плоскость этого двугранного угла. Поэтому центр сферы, вписанной в тетраэдр, равноудалён от всех граней пирамиды, он принадлежит каждой из биссекторных плоскостей, т.е. он – точка пересечения биссекторных плоскостей всех двугранных углов тетраэдра. Центр сферы, вписанной в тетраэдр, всегда находится внутри тетраэдра, т.к. все точки биссекторной плоскости расположены между гранями двугранного угла.
Таким образом, центр у вписанной сферы может быть только один. Сфера с центром в этой точке и радиусом, равным расстоянию от этой точки до плоскости какой-либо грани тетраэдра, касается всех граней тетраэдра. Значит, в любой тетраэдр можно вписать сферу и притом только одну.
Осталось лишь доказать, что биссекторные плоскости двугранных углов тетраэдра пересекаются в одной точке.
См. Рис.2
M лежит на γ. Угол АСВ – линейный угол двугранного угла между плоскостями α и β.
Пусть γ делит этот угол так, что углы ВСМ и АСМ равны, т.е. γ – биссекторная плоскость. Докажем, что биссекторные плоскости двугранных углов трёхгранного угла пересекаются по одному лучу.
См. Рис.3
β1 и β2 – биссекторные плоскости, их пересечение – луч l, исходящий из вершины S тетраэдра. Пусть А, принадлежащая l, произвольная точка луча. Проведём перпендикуляры AA1, AA2, AA3 на грани трёхгранного угла. A принадлежит β1, поэтому АА2 = AA1; A принадлежит β2, поэтому АА3 = AA1.
Значит AA1 = AA2 = AA3, т.е. А равноудалена от плоскостей граней NSP и MSP. Значит, А находится на биссеторной плоскости двугранного угла с ребром SP. Т.к. мы выбирали А произвольно, значит, весь луч находится в биссекторной плоскости. Значит, все три биссекторные плоскости пересекаются по одному лучу, любая точка которых равноудалена.
См. Рис.4
Пусть l – луч, по которому пересекаются биссекторные плоскости трёхгранного угла при вершине А, М – точка, в которой l пересекает BDC. Концы АМ принадлежат разным граням двугранного угла при ребре ВС, поэтому биссекторная плоскость этого двугранного угла пересечёт отрезок АМ в точке О. О лежит на l, поэтому она равноудалена от плоскостей ABC, ABD и ACD. Кроме этого, расстояние от О до ABC и BCD равны, т.к. О принадлежит биссекторной плоскости двугранного угла при ребре ВС. Значит, О равноудалена от всех граней тетраэдра, т.е. принадлежит всем биссекторным плоскостям двугранных углов тетраэдра. Итак, биссекторные плоскости двугранных углов тетраэдра пересекаются в одной точке.
а) См. Рис.1
Будем доказывать, что через любые 4 точки, не лежащие в одной плоскости, можно провести сферу, и притом только одну. Центр сферы, описанной около тетраэдра, должен принадлежать каждой из плоскостей, проведённых через середины рёбер тетраэдра перпендикулярно к его рёбрам.
Пусть О – центр окружности, описанной около грани АВС, l – прямая, проходит через О и перпендикулярна плоскости АВС. Каждая точка l равноудалена от точек А, В, С. (ОА = ОВ = ОС = r – радиус описанной окружности). Если S лежит на l, то ∆SOA = ∆SOB = ∆SOC (по двум катетам). Значит, SA = SB = SC.
Пусть плоскость α проходит через середину DA и перпендикулярна DA. Нужно доказать, что l и α пересекаются. Предположим, что это не так, т.е. что они параллельны.
Если α ⊥AD и l || α, то AD ⊥l. Но l ⊥AB и, тогда, l ⊥ABD (по признаку перпендикулярности прямой плоскости).
Значит, через одну точку были проведены две разные плоскости, перпендикулярные к одной прямой. Наше предположение неверно, т.е. l и α пересекаются. Пусть S – их точка пересечения. Тогда SD = SA. Т.к. S лежит на l, то SA = SB = SC, и, следовательно, S равноудалена от всех вершин тетраэдра.
Обозначим через R расстояние от О до одной из вершин тетраэдра. Сфера с центром в S и радиусом R проходит через все данные точки. Из доказанного выше следует, что такая сфера может быть только одна.
Таким образом, доказали, что около любого тетраэдра можно описать сферу
б) Будем рассматривать 2 грани с общим ребром. Геометрическим местом точек, равноудалённых от обеих граней двугранного угла, будет плоскость, делящая двугранный угол пополам, или, другими словами, биссекторная плоскость этого двугранного угла. Поэтому центр сферы, вписанной в тетраэдр, равноудалён от всех граней пирамиды, он принадлежит каждой из биссекторных плоскостей, т.е. он – точка пересечения биссекторных плоскостей всех двугранных углов тетраэдра. Центр сферы, вписанной в тетраэдр, всегда находится внутри тетраэдра, т.к. все точки биссекторной плоскости расположены между гранями двугранного угла.
Таким образом, центр у вписанной сферы может быть только один. Сфера с центром в этой точке и радиусом, равным расстоянию от этой точки до плоскости какой-либо грани тетраэдра, касается всех граней тетраэдра. Значит, в любой тетраэдр можно вписать сферу и притом только одну.
Осталось лишь доказать, что биссекторные плоскости двугранных углов тетраэдра пересекаются в одной точке.
См. Рис.2
M лежит на γ. Угол АСВ – линейный угол двугранного угла между плоскостями α и β.
Пусть γ делит этот угол так, что углы ВСМ и АСМ равны, т.е. γ – биссекторная плоскость. Докажем, что биссекторные плоскости двугранных углов трёхгранного угла пересекаются по одному лучу.
См. Рис.3
β1 и β2 – биссекторные плоскости, их пересечение – луч l, исходящий из вершины S тетраэдра. Пусть А, принадлежащая l, произвольная точка луча. Проведём перпендикуляры AA1, AA2, AA3 на грани трёхгранного угла. A принадлежит β1, поэтому АА2 = AA1; A принадлежит β2, поэтому АА3 = AA1.
Значит AA1 = AA2 = AA3, т.е. А равноудалена от плоскостей граней NSP и MSP. Значит, А находится на биссеторной плоскости двугранного угла с ребром SP. Т.к. мы выбирали А произвольно, значит, весь луч находится в биссекторной плоскости. Значит, все три биссекторные плоскости пересекаются по одному лучу, любая точка которых равноудалена.
См. Рис.4
Пусть l – луч, по которому пересекаются биссекторные плоскости трёхгранного угла при вершине А, М – точка, в которой l пересекает BDC. Концы АМ принадлежат разным граням двугранного угла при ребре ВС, поэтому биссекторная плоскость этого двугранного угла пересечёт отрезок АМ в точке О. О лежит на l, поэтому она равноудалена от плоскостей ABC, ABD и ACD. Кроме этого, расстояние от О до ABC и BCD равны, т.к. О принадлежит биссекторной плоскости двугранного угла при ребре ВС. Значит, О равноудалена от всех граней тетраэдра, т.е. принадлежит всем биссекторным плоскостям двугранных углов тетраэдра. Итак, биссекторные плоскости двугранных углов тетраэдра пересекаются в одной точке.
Будем доказывать, что через любые 4 точки, не лежащие в одной плоскости, можно провести сферу, и притом только одну. Центр сферы, описанной около тетраэдра, должен принадлежать каждой из плоскостей, проведённых через середины рёбер тетраэдра перпендикулярно к его рёбрам.
Пусть О – центр окружности, описанной около грани АВС, l – прямая, проходит через О и перпендикулярна плоскости АВС. Каждая точка l равноудалена от точек А, В, С. (ОА = ОВ = ОС = r – радиус описанной окружности). Если S лежит на l, то ∆SOA = ∆SOB = ∆SOC (по двум катетам). Значит, SA = SB = SC.
Пусть плоскость α проходит через середину DA и перпендикулярна DA. Нужно доказать, что l и α пересекаются. Предположим, что это не так, т.е. что они параллельны.
Если α ⊥AD и l || α, то AD ⊥l. Но l ⊥AB и, тогда, l ⊥ABD (по признаку перпендикулярности прямой плоскости).
Значит, через одну точку были проведены две разные плоскости, перпендикулярные к одной прямой. Наше предположение неверно, т.е. l и α пересекаются. Пусть S – их точка пересечения. Тогда SD = SA. Т.к. S лежит на l, то SA = SB = SC, и, следовательно, S равноудалена от всех вершин тетраэдра.
Обозначим через R расстояние от О до одной из вершин тетраэдра. Сфера с центром в S и радиусом R проходит через все данные точки. Из доказанного выше следует, что такая сфера может быть только одна.
Таким образом, доказали, что около любого тетраэдра можно описать сферу
б) Будем рассматривать 2 грани с общим ребром. Геометрическим местом точек, равноудалённых от обеих граней двугранного угла, будет плоскость, делящая двугранный угол пополам, или, другими словами, биссекторная плоскость этого двугранного угла. Поэтому центр сферы, вписанной в тетраэдр, равноудалён от всех граней пирамиды, он принадлежит каждой из биссекторных плоскостей, т.е. он – точка пересечения биссекторных плоскостей всех двугранных углов тетраэдра. Центр сферы, вписанной в тетраэдр, всегда находится внутри тетраэдра, т.к. все точки биссекторной плоскости расположены между гранями двугранного угла.
Таким образом, центр у вписанной сферы может быть только один. Сфера с центром в этой точке и радиусом, равным расстоянию от этой точки до плоскости какой-либо грани тетраэдра, касается всех граней тетраэдра. Значит, в любой тетраэдр можно вписать сферу и притом только одну.
Осталось лишь доказать, что биссекторные плоскости двугранных углов тетраэдра пересекаются в одной точке.
См. Рис.2
M лежит на γ. Угол АСВ – линейный угол двугранного угла между плоскостями α и β.
Пусть γ делит этот угол так, что углы ВСМ и АСМ равны, т.е. γ – биссекторная плоскость. Докажем, что биссекторные плоскости двугранных углов трёхгранного угла пересекаются по одному лучу.
См. Рис.3
β1 и β2 – биссекторные плоскости, их пересечение – луч l, исходящий из вершины S тетраэдра. Пусть А, принадлежащая l, произвольная точка луча. Проведём перпендикуляры AA1, AA2, AA3 на грани трёхгранного угла. A принадлежит β1, поэтому АА2 = AA1; A принадлежит β2, поэтому АА3 = AA1.
Значит AA1 = AA2 = AA3, т.е. А равноудалена от плоскостей граней NSP и MSP. Значит, А находится на биссеторной плоскости двугранного угла с ребром SP. Т.к. мы выбирали А произвольно, значит, весь луч находится в биссекторной плоскости. Значит, все три биссекторные плоскости пересекаются по одному лучу, любая точка которых равноудалена.
См. Рис.4
Пусть l – луч, по которому пересекаются биссекторные плоскости трёхгранного угла при вершине А, М – точка, в которой l пересекает BDC. Концы АМ принадлежат разным граням двугранного угла при ребре ВС, поэтому биссекторная плоскость этого двугранного угла пересечёт отрезок АМ в точке О. О лежит на l, поэтому она равноудалена от плоскостей ABC, ABD и ACD. Кроме этого, расстояние от О до ABC и BCD равны, т.к. О принадлежит биссекторной плоскости двугранного угла при ребре ВС. Значит, О равноудалена от всех граней тетраэдра, т.е. принадлежит всем биссекторным плоскостям двугранных углов тетраэдра. Итак, биссекторные плоскости двугранных углов тетраэдра пересекаются в одной точке.



