Задание
Развернуть задание
В правильной четырёхугольной пирамиде радиусы вписанной и описанной сферы равны 2 см и 5 см. Найдите сторону основания и высоту пирамиды.
Развернуть задание
Новое решение
Решение
См. Рис.1
Продолжим высоту пирамиды РН до пересечения со сферой в точке Q. PQ – диаметр. Соединим точку А с точкой Н. Рассмотрим сечение плоскостью APQ.
Угол QAP = 90^0, так как он опирается на диаметр. Треугольники НРА и HAQ подобны, AH/PH = HQ/AH, AH^2 = HQ*PH, PQ = 10, PH = h
Пусть а – сторона основания, тогда АН = ½*a*sqrt(2) = a*sqrt(2)/2
Значит:
a^2/2 = h*(10 - h)
См. Рис.2
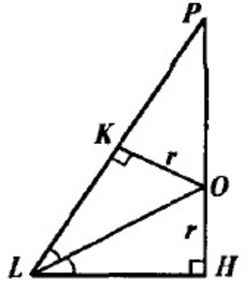
Проведём HL⊥AB и отрезок PL. LH = a/2, плоскость PLH перпендикулярна плоскости АВР. Пусть О – центр вписанной сферы, ОК⊥PL. OH = OK = r, OL – биссектриса угла HLP. По т. Пифагора: PL = sqrt(h^2 + LH^2) = sqrt(h^2 + a^2/4)
Пусть угол HLP = α
sinα = PH/LP = h/sqrt(h^2+a^2/4) = 2h/sqrt(4h^2+a^2)
cosα = LH/PL = a/2/sqrt(h^2+a^2/4) = a/sqrt(4h^2+a^2)
Из ∆OLH: OH/LH = r/a = 2r/a = tg(α/2), r=a/2* tg(α/2) = 2
tg(α/2) = (1 – cosα)/sinα = (1 - a/sqrt(4h^2+a^2))/( 2h/sqrt(4h^2+a^2)) = (sqrt(4h^2 - a^2) – a)/2h
a/2*(sqrt(4h^2 + a^2) – a)/2h = 2
Получили систему:
a*sqrt(4h^2 + a^2) = a^2 + 8h
a^2 = 2р(10 – h)
a^2*(4h^2 + a^2) = a^4 + 64*h^2 + 16*a^2*h
a^2*(4 – h) + 16*h = 0
2h*(10 - h)*(4 - h) + 16*h =0
Разделим обе части на 2*h:
(10 - h)*(4 - h) + 8 =0
h^2 – 14*h + 48 = 0
h1 = 8 или h2 = 6
a1^2 = 20*8 – 2*64 = 32
a1 = 4*sqrt(2)
a2^2 = 20*6 – 2*36 = 48
a2 = 4*sqrt(3)
Продолжим высоту пирамиды РН до пересечения со сферой в точке Q. PQ – диаметр. Соединим точку А с точкой Н. Рассмотрим сечение плоскостью APQ.
Угол QAP = 90^0, так как он опирается на диаметр. Треугольники НРА и HAQ подобны, AH/PH = HQ/AH, AH^2 = HQ*PH, PQ = 10, PH = h
Пусть а – сторона основания, тогда АН = ½*a*sqrt(2) = a*sqrt(2)/2
Значит:
a^2/2 = h*(10 - h)
См. Рис.2
Проведём HL⊥AB и отрезок PL. LH = a/2, плоскость PLH перпендикулярна плоскости АВР. Пусть О – центр вписанной сферы, ОК⊥PL. OH = OK = r, OL – биссектриса угла HLP. По т. Пифагора: PL = sqrt(h^2 + LH^2) = sqrt(h^2 + a^2/4)
Пусть угол HLP = α
sinα = PH/LP = h/sqrt(h^2+a^2/4) = 2h/sqrt(4h^2+a^2)
cosα = LH/PL = a/2/sqrt(h^2+a^2/4) = a/sqrt(4h^2+a^2)
Из ∆OLH: OH/LH = r/a = 2r/a = tg(α/2), r=a/2* tg(α/2) = 2
tg(α/2) = (1 – cosα)/sinα = (1 - a/sqrt(4h^2+a^2))/( 2h/sqrt(4h^2+a^2)) = (sqrt(4h^2 - a^2) – a)/2h
a/2*(sqrt(4h^2 + a^2) – a)/2h = 2
Получили систему:
a*sqrt(4h^2 + a^2) = a^2 + 8h
a^2 = 2р(10 – h)
a^2*(4h^2 + a^2) = a^4 + 64*h^2 + 16*a^2*h
a^2*(4 – h) + 16*h = 0
2h*(10 - h)*(4 - h) + 16*h =0
Разделим обе части на 2*h:
(10 - h)*(4 - h) + 8 =0
h^2 – 14*h + 48 = 0
h1 = 8 или h2 = 6
a1^2 = 20*8 – 2*64 = 32
a1 = 4*sqrt(2)
a2^2 = 20*6 – 2*36 = 48
a2 = 4*sqrt(3)
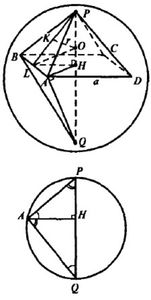
См. Рис.1
Продолжим высоту пирамиды РН до пересечения со сферой в точке Q. PQ – диаметр. Соединим точку А с точкой Н. Рассмотрим сечение плоскостью APQ.
Угол QAP = 90^0, так как он опирается на диаметр. Треугольники НРА и HAQ подобны, AH/PH = HQ/AH, AH^2 = HQ*PH, PQ = 10, PH = h
Пусть а – сторона основания, тогда АН = ½*a*sqrt(2) = a*sqrt(2)/2
Значит:
a^2/2 = h*(10 - h)
См. Рис.2
Проведём HL⊥AB и отрезок PL. LH = a/2, плоскость PLH перпендикулярна плоскости АВР. Пусть О – центр вписанной сферы, ОК⊥PL. OH = OK = r, OL – биссектриса угла HLP. По т. Пифагора: PL = sqrt(h^2 + LH^2) = sqrt(h^2 + a^2/4)
Пусть угол HLP = α
sinα = PH/LP = h/sqrt(h^2+a^2/4) = 2h/sqrt(4h^2+a^2)
cosα = LH/PL = a/2/sqrt(h^2+a^2/4) = a/sqrt(4h^2+a^2)
Из ∆OLH: OH/LH = r/a = 2r/a = tg(α/2), r=a/2* tg(α/2) = 2
tg(α/2) = (1 – cosα)/sinα = (1 - a/sqrt(4h^2+a^2))/( 2h/sqrt(4h^2+a^2)) = (sqrt(4h^2 - a^2) – a)/2h
a/2*(sqrt(4h^2 + a^2) – a)/2h = 2
Получили систему:
a*sqrt(4h^2 + a^2) = a^2 + 8h
a^2 = 2р(10 – h)
a^2*(4h^2 + a^2) = a^4 + 64*h^2 + 16*a^2*h
a^2*(4 – h) + 16*h = 0
2h*(10 - h)*(4 - h) + 16*h =0
Разделим обе части на 2*h:
(10 - h)*(4 - h) + 8 =0
h^2 – 14*h + 48 = 0
h1 = 8 или h2 = 6
a1^2 = 20*8 – 2*64 = 32
a1 = 4*sqrt(2)
a2^2 = 20*6 – 2*36 = 48
a2 = 4*sqrt(3)
Продолжим высоту пирамиды РН до пересечения со сферой в точке Q. PQ – диаметр. Соединим точку А с точкой Н. Рассмотрим сечение плоскостью APQ.
Угол QAP = 90^0, так как он опирается на диаметр. Треугольники НРА и HAQ подобны, AH/PH = HQ/AH, AH^2 = HQ*PH, PQ = 10, PH = h
Пусть а – сторона основания, тогда АН = ½*a*sqrt(2) = a*sqrt(2)/2
Значит:
a^2/2 = h*(10 - h)
См. Рис.2
Проведём HL⊥AB и отрезок PL. LH = a/2, плоскость PLH перпендикулярна плоскости АВР. Пусть О – центр вписанной сферы, ОК⊥PL. OH = OK = r, OL – биссектриса угла HLP. По т. Пифагора: PL = sqrt(h^2 + LH^2) = sqrt(h^2 + a^2/4)
Пусть угол HLP = α
sinα = PH/LP = h/sqrt(h^2+a^2/4) = 2h/sqrt(4h^2+a^2)
cosα = LH/PL = a/2/sqrt(h^2+a^2/4) = a/sqrt(4h^2+a^2)
Из ∆OLH: OH/LH = r/a = 2r/a = tg(α/2), r=a/2* tg(α/2) = 2
tg(α/2) = (1 – cosα)/sinα = (1 - a/sqrt(4h^2+a^2))/( 2h/sqrt(4h^2+a^2)) = (sqrt(4h^2 - a^2) – a)/2h
a/2*(sqrt(4h^2 + a^2) – a)/2h = 2
Получили систему:
a*sqrt(4h^2 + a^2) = a^2 + 8h
a^2 = 2р(10 – h)
a^2*(4h^2 + a^2) = a^4 + 64*h^2 + 16*a^2*h
a^2*(4 – h) + 16*h = 0
2h*(10 - h)*(4 - h) + 16*h =0
Разделим обе части на 2*h:
(10 - h)*(4 - h) + 8 =0
h^2 – 14*h + 48 = 0
h1 = 8 или h2 = 6
a1^2 = 20*8 – 2*64 = 32
a1 = 4*sqrt(2)
a2^2 = 20*6 – 2*36 = 48
a2 = 4*sqrt(3)

