Решения
Алиса


07-12-2016 00:06

0
Задания
Задание
Екатерина
06-12-2016
20:46
Школа

Геометрия

11 класс


11
1
0
0

Формула объема цилиндра

Найти объём цилиндра.

Развернуть задание
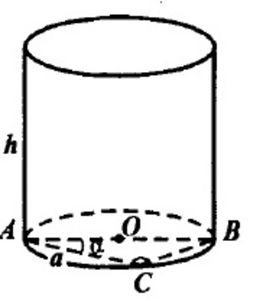
В цилиндр вписана призма, основанием которой является прямоугольный треугольник с катетом а и прилежащим к нему углом α. Найдите объём цилиндра, если высота призмы равна h.
Сергей Геннадиевич
Новый коммент
24-07-2017 17:41:17
Алиса
Судя по таблице удельной теплоёмкости, это может быть цинк.
22-11-2016 12:57:23
Анастасия
Дмитрий Да, перевод обязателен.
21-11-2016 19:00:39
Дмитрий
1) –Обязательно ли переводить массу мяча в СИ?
21-11-2016 18:51:12
Рогова Дарья
Условие смущает. Ладно, пусть время будет отрицательным, наблюдать можно с любого момента, но не ясно, каким моментам времени соответствуют моменты изменения скорости. Можно предположить, что первый пик где-то в районе -1,5 с, но так ли это?.. Третий пик вообще без координатной сетки не определишь. И еще: график чего именно надо построить? МОДУЛЯ скорости или ПРОЕКЦИИ скорости?
3-11-2016 00:11:19
Андрей Анатольевич
Почему картика в блоке так размыта? А при просмотре в правой части (крупно) все выглядит гораздо лучше. Как то плохо пережимается картинка.
2-11-2016 15:29:02
Андрей Анатольевич
t = 20ºC или 200 С ?
31-10-2016 20:21:46
Эдуард Блохин
Интересное задание. Пригодится.
27-10-2016 14:34:02
Развернуть задание
Новое решение
Сложность
4 3 2 1
Решение
Алиса
7-12-2016 00:06:50
0
Угол С = 90^0. Угол АСВ – вписанный и равен 90^0, значит, он опирается на диаметр АВ. АВ = 2*r = a/cosα; r = a/2cosα, r – радиус основания цилиндра
Высота призмы равна высоте цилиндра, поэтому:
V_ц = π*r^2*h = π* h *a^2 / 4(cosα)^2
Лолита
Алиса Если окружность вписана в правильный шестиугольник, как в нашем случае, то формула такая: √3/2 * a, где a – сторона шестиугольника.
29-11-2016 23:31:14
Лолита
Алиса Земля похожа на шар, но немного приплюснута с полюсов.
29-11-2016 23:30:28
Алина
Анастасия Обычно его представляют, как число 3.14. А получается π из отношения длины окружности к длине её диаметра.
29-11-2016 23:28:54
Дмитрий
Диана Это произведение его длины и ширины.
29-11-2016 23:28:33
Диана
Что такое площадь прямоугольного участка?
29-11-2016 23:27:49
Алина
Дмитрий Это – минуты. Градус делят на 60 минут, а минуту на 60 секунд, как в часах.
29-11-2016 23:27:42
Диана
Алина Это сумма всех его сторон.
29-11-2016 23:27:08
Елизавета
Диана Если закрепить маятник в какой-то точке, то, натянув нить, свободный конец маятника
будет описывать вокруг этой точки окружность, длина этого маятника как раз и будет радиусом этой окружности.
29-11-2016 23:26:13
Алина
Что такое периметр прямоугольника?
29-11-2016 23:26:06
Елизавета
Екатерина Расстояние, которое проходит колесо за один оборот. Или же, если говорить иначе, длина окружности колеса.
29-11-2016 23:25:29
Дмитрий
Ира Это просто. Если от площади внешнего круга отнять площадь внутреннего круга, то останется кусок внешнего круга, представляющий собой именно кольцо. Отсюда и формула.
29-11-2016 23:24:13
Дмитрий
Влада Градусная мера дуги, т.е. величина угла, который образует эту дугу.
29-11-2016 23:23:25
Дмитрий
Екатерина Точка пересечения медиан делит каждую из них в отношении 2:1, считая от вершины.
29-11-2016 23:22:42
Катя
Лолита К последнему действию мы имеем радиус отверстия и радиус нашей проволоки.
Радиус проволоки больше, значит, чтобы узнать, насколько нужно уменьшить её радиус, чтобы она влезла, нужно вычесть из её радиуса радиус отверстия.
29-11-2016 23:21:04
Катя
Ира Именно так.
29-11-2016 23:20:25
Катя
Лолита S = 3/2 * a^2 * √3, где a – сторона шестиугольника.
29-11-2016 23:19:51
Ира
Ольга Да, именно она.
29-11-2016 23:18:40
Екатерина
Лолита Если запихнуть дрова в машину, то она вообще не поедет :)
29-11-2016 23:18:28
Ира
Дмитрий По условию нам нужно из бруска вытачивать круглый стержень, то есть обрезать брусок, пока он не станет круглым, а значит окружность должна быть вписанной.
29-11-2016 23:17:57
Анастасия
Чему равно π?
29-11-2016 23:15:58
Алиса
7-12-2016 00:06:50
0
Угол С = 90^0. Угол АСВ – вписанный и равен 90^0, значит, он опирается на диаметр АВ. АВ = 2*r = a/cosα; r = a/2cosα, r – радиус основания цилиндра
Высота призмы равна высоте цилиндра, поэтому:
V_ц = π*r^2*h = π* h *a^2 / 4(cosα)^2
Новость часа

Форма обратной связи