Задание
Развернуть задание
Два девятых класса одной школы приобрели билеты в театр. Первый класс израсходовал на билеты 4900₽. Второй класс купил на 15 билетов меньше, но заплатил за каждый билет на 35₽ дороже и потратил на билеты 3500₽. Сколько билетов и по какой цене куплено каждым классом?
Развернуть задание
Новое решение
Решение
1. Пусть x ₽ - цена билета 1-го класса, y- количество билетов 1-го класса.
2. Тогда, по условию, 1-й класс израсходовал x*y=4900. 2-й класс израсходовал (x + 35) * (y - 15) = 3500
3. Составим систему уравнений
2. Тогда, по условию, 1-й класс израсходовал x*y=4900. 2-й класс израсходовал (x + 35) * (y - 15) = 3500
3. Составим систему уравнений
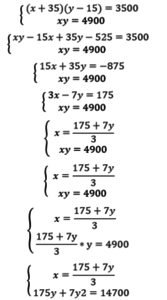
Решая уравнение y^2 – 25x – 2100 = 0, получаем: D = (-25)^2 – 4 *(-2100) = 9025
y1, y2 = (25 ± 95)/2 => y1 =35, y2 = -60 (не подходит так как кол-во билетов не может быть отрицательным).
x = (175 + 7y)/3 = (175 + 7*35)/3 = 140
4. Найдем кол-во билетов и стоимость билета для 2-го класса:
35 – 15 = 20 кол-во билетов.
35 + 140 = 175₽.
Ответ: кол-во билетов и стоимость билета для 1-го класса - 35 и 140₽, кол-во билетов и стоимость билета для 2-го класса – 20 и 175₽.
y1, y2 = (25 ± 95)/2 => y1 =35, y2 = -60 (не подходит так как кол-во билетов не может быть отрицательным).
x = (175 + 7y)/3 = (175 + 7*35)/3 = 140
4. Найдем кол-во билетов и стоимость билета для 2-го класса:
35 – 15 = 20 кол-во билетов.
35 + 140 = 175₽.
Ответ: кол-во билетов и стоимость билета для 1-го класса - 35 и 140₽, кол-во билетов и стоимость билета для 2-го класса – 20 и 175₽.
1. Пусть x ₽ - цена билета 1-го класса, y- количество билетов 1-го класса.
2. Тогда, по условию, 1-й класс израсходовал x*y=4900. 2-й класс израсходовал (x + 35) * (y - 15) = 3500
3. Составим систему уравнений
2. Тогда, по условию, 1-й класс израсходовал x*y=4900. 2-й класс израсходовал (x + 35) * (y - 15) = 3500
3. Составим систему уравнений

Решая уравнение y^2 – 25x – 2100 = 0, получаем: D = (-25)^2 – 4 *(-2100) = 9025
y1, y2 = (25 ± 95)/2 => y1 =35, y2 = -60 (не подходит так как кол-во билетов не может быть отрицательным).
x = (175 + 7y)/3 = (175 + 7*35)/3 = 140
4. Найдем кол-во билетов и стоимость билета для 2-го класса:
35 – 15 = 20 кол-во билетов.
35 + 140 = 175₽.
Ответ: кол-во билетов и стоимость билета для 1-го класса - 35 и 140₽, кол-во билетов и стоимость билета для 2-го класса – 20 и 175₽.
y1, y2 = (25 ± 95)/2 => y1 =35, y2 = -60 (не подходит так как кол-во билетов не может быть отрицательным).
x = (175 + 7y)/3 = (175 + 7*35)/3 = 140
4. Найдем кол-во билетов и стоимость билета для 2-го класса:
35 – 15 = 20 кол-во билетов.
35 + 140 = 175₽.
Ответ: кол-во билетов и стоимость билета для 1-го класса - 35 и 140₽, кол-во билетов и стоимость билета для 2-го класса – 20 и 175₽.