Задание
Развернуть задание
Катер по реке и автобус по дороге, идущей вдоль берега реки, отправляются одновременно из пункта А в пункт В и совершаю безостановочное движение между А и В. Первая встреча их произошла, когда автобус прошел 5/9 всего расстояния от А до В, а вторая встреча - когда автобус после первого захода в В проехал ⅛ всего расстояния от В до А. Первый раз в пункт В автобус прибыл на 16 мин позже катера. Через сколько часов после начала движения автобус и катер первый раз окажутся одновременно в пункте А?
Развернуть задание
Новое решение
Решение
1) Пусть s - расстояние от А до В. t0, t1 - время прохождение пути АВ соответственно автобусом и катером. t1 - время, за которое катер проходит путь от В до А.
2) По условию 5/9t0=t1+4/9t2 ; 9/8t0=t1+t2+⅞ * t1 ; t0=t1+4/15.
3) Решим систему уравнений:
2) По условию 5/9t0=t1+4/9t2 ; 9/8t0=t1+t2+⅞ * t1 ; t0=t1+4/15.
3) Решим систему уравнений:
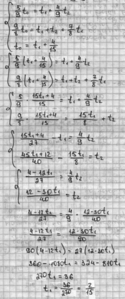
4) Получаем t0 = ⅖ ; t1 = 2/15; t2 = ⅕
5) Автобус прибывает в пункт А, выполнив четное число рейсов (m от А до В и m от B до А) и затрачивает при этом время 2mt0. Возвращаясь в пункт А, катер делает тоже четное число 2n рейсов и затрачивает время nt1+nt2=n(t1+t2). Автобус и катер одновременно могут оказаться в пункте А, когда найдутся натуральные числа m и n, такие что 2mt0=n(t1+t2) ⇔ 4/5m=1/3n ⇔ n=12/5m. Наименьшее возможное натуральное число n=12, значит m=5 => 2mt0=n(t1+t2) =4 ч
Ответ: 4 ч
5) Автобус прибывает в пункт А, выполнив четное число рейсов (m от А до В и m от B до А) и затрачивает при этом время 2mt0. Возвращаясь в пункт А, катер делает тоже четное число 2n рейсов и затрачивает время nt1+nt2=n(t1+t2). Автобус и катер одновременно могут оказаться в пункте А, когда найдутся натуральные числа m и n, такие что 2mt0=n(t1+t2) ⇔ 4/5m=1/3n ⇔ n=12/5m. Наименьшее возможное натуральное число n=12, значит m=5 => 2mt0=n(t1+t2) =4 ч
Ответ: 4 ч
1) Пусть s - расстояние от А до В. t0, t1 - время прохождение пути АВ соответственно автобусом и катером. t1 - время, за которое катер проходит путь от В до А.
2) По условию 5/9t0=t1+4/9t2 ; 9/8t0=t1+t2+⅞ * t1 ; t0=t1+4/15.
3) Решим систему уравнений:
2) По условию 5/9t0=t1+4/9t2 ; 9/8t0=t1+t2+⅞ * t1 ; t0=t1+4/15.
3) Решим систему уравнений:
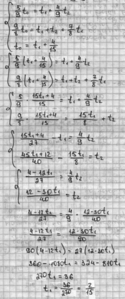
4) Получаем t0 = ⅖ ; t1 = 2/15; t2 = ⅕
5) Автобус прибывает в пункт А, выполнив четное число рейсов (m от А до В и m от B до А) и затрачивает при этом время 2mt0. Возвращаясь в пункт А, катер делает тоже четное число 2n рейсов и затрачивает время nt1+nt2=n(t1+t2). Автобус и катер одновременно могут оказаться в пункте А, когда найдутся натуральные числа m и n, такие что 2mt0=n(t1+t2) ⇔ 4/5m=1/3n ⇔ n=12/5m. Наименьшее возможное натуральное число n=12, значит m=5 => 2mt0=n(t1+t2) =4 ч
Ответ: 4 ч
5) Автобус прибывает в пункт А, выполнив четное число рейсов (m от А до В и m от B до А) и затрачивает при этом время 2mt0. Возвращаясь в пункт А, катер делает тоже четное число 2n рейсов и затрачивает время nt1+nt2=n(t1+t2). Автобус и катер одновременно могут оказаться в пункте А, когда найдутся натуральные числа m и n, такие что 2mt0=n(t1+t2) ⇔ 4/5m=1/3n ⇔ n=12/5m. Наименьшее возможное натуральное число n=12, значит m=5 => 2mt0=n(t1+t2) =4 ч
Ответ: 4 ч