Задание
Развернуть задание
Бассейн наполняется водой из 2 кранов. Сначала 1-ый кран был открыт одну треть того времени, которое требуется для наполнения бассейна только через один второй кран. Затем, наоборот, второй кран был открыт одну треть того времени, которое требуется для наполнения бассейна через один первый кран. После этого оказалось что наполнены 13/18 всего бассейна. Оба крана наполняют бассейн за 3 часа 36 минут. Сколько времени потребуется для наполнения бассейна каждым краном в отдельности?
Развернуть задание
Новое решение
Решение
1. Пусть x ч. - время, за которое полностью заполняет бассейн 1-й кран, y ч.- время, за которое полностью заполняет бассейн 2-й кран. Значит 1/x- производительность 1-го крана, 1/y - производительность 2-го крана.
2. Тогда, по условию: (1/x + 1/y) * 3.6 = 1; x/(3y) + y/(3x) = 13/18
3. Составим систему уравнений:
2. Тогда, по условию: (1/x + 1/y) * 3.6 = 1; x/(3y) + y/(3x) = 13/18
3. Составим систему уравнений:
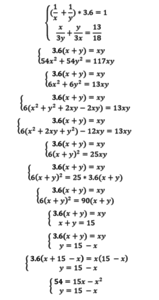
Решая уравнение x^2 – 15x + 54 = 0, получаем: D = (-15)^2 – 4 *(54) = 9
x1, x2 = (15 ± 3)/2 => x1 = 9, x2 = 6
y1 = 15 – x1 = 6
y2 = 15 – x2 = 9
Ответ: 6ч. и 9ч.
x1, x2 = (15 ± 3)/2 => x1 = 9, x2 = 6
y1 = 15 – x1 = 6
y2 = 15 – x2 = 9
Ответ: 6ч. и 9ч.
1. Пусть x ч. - время, за которое полностью заполняет бассейн 1-й кран, y ч.- время, за которое полностью заполняет бассейн 2-й кран. Значит 1/x- производительность 1-го крана, 1/y - производительность 2-го крана.
2. Тогда, по условию: (1/x + 1/y) * 3.6 = 1; x/(3y) + y/(3x) = 13/18
3. Составим систему уравнений:
2. Тогда, по условию: (1/x + 1/y) * 3.6 = 1; x/(3y) + y/(3x) = 13/18
3. Составим систему уравнений:
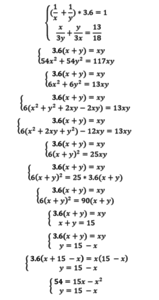
Решая уравнение x^2 – 15x + 54 = 0, получаем: D = (-15)^2 – 4 *(54) = 9
x1, x2 = (15 ± 3)/2 => x1 = 9, x2 = 6
y1 = 15 – x1 = 6
y2 = 15 – x2 = 9
Ответ: 6ч. и 9ч.
x1, x2 = (15 ± 3)/2 => x1 = 9, x2 = 6
y1 = 15 – x1 = 6
y2 = 15 – x2 = 9
Ответ: 6ч. и 9ч.